Фізичний маятник. Фізичним маятником

називається тверде тіло, що може обертатися під дією сили O l

тяжіння відносно нерухомої осі, що не проходить через центр j

тяжіння тіла. При відхиленні маятника від положення

рівноваги на кут j виникає момент сили, що прагне повернути C

маятник у положення рівноваги. Цей момент дорівнює

M = - mgl sin j, (26.12)

де m – маса маятника, а l – відстань від точки підвісу O до центра мас маятника C (рис. 26.3). Знак мінус пов’язаний з тим,

що момент сили діє так, щоб повернути тверде тіло у положення mg

рівноваги.

Позначивши момент інерції маятника відносно осі, що проходить через точку підвісу O, через I, можна написати

I jÿÿ = - mgl sin j. (26.13)

Рисунок 26.3 – Фізичний маятник: l – відстань від точки підвісу до центра мас C

У випадку малих коливань (j << 1,

рівняння гармонічних коливань:

sin j» j) рівняння (26.13) переходить у диференціальне

jÿÿ + w2j = 0

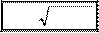де

, (26.14)

w0=

mgl / I

. (26.15)

З формул (26.14) і (26.15) випливає, що при малих відхиленнях від положення рівноваги фізичний маятник виконує гармонічні коливання, частота яких залежить від маси маятника, моменту інерції маятника відносно осі підвісу й відстані від точки O підвісу до центра мас C маятника. Використовуючи (26.15) неважко знайти період коливань фізичного маятника:

T = 2p / w0 = 2p

I / mgl. (26.16)

За теоремою Штейнера момент інерції маятника I може бути поданий у вигляді

I = IC

+ ml 2,

де IC

– момент інерції відносно осі, яка паралельна осі підвісу й проходить через центр мас

C. Тоді циклічна частота (26.15) й період коливань (26.16) можуть бути подані у вигляді

w0=

mgl /(IC

+ ml 2),

T = 2p

(IC

+ ml 2)/(mgl). (26.17)

§ 27 Електричний коливальний контур. Частота коливань [5]

1 При розгляді електричних коливань ми маємо справу зі струмами, що змінюються у часі. Закон Ома й правила Кірхгофа були встановлені для постійного струму. Однак вони залишаються справедливими й для миттєвих значень змінних струмів і напруг, якщо тільки їх зміни відбуваються не занадто швидко. Електромагнітні збурювання поширюються вздовж електричного кола з величезною швидкістю, що дорівнює швидкості світла c. Якщо

за час

t = l / c

(l – довжина кола, c – швидкість світла), який необхідний для передачі

збурення в найвіддаленішу точку кола, сила змінного струму майже не змінюється, то

миттєві значення сили струму у всіх перерізах кола можна вважати однаковими. Струми, що задовольняють таку умову, називаються квазістаціонарними. Для періодично змінних струмів умова квазістаціонарності має вигляд

t = l / c << T,

де T – період коливальних процесів. Миттєві значення квазістаціонарних струмів задовольняють закон Ома. Отже, для них справедливі й правила Кірхгофа. При вивченні електричних коливань ми будемо припускати, що розглянуті нами струми є квазістаціонарними.

2 Коливальним контуром називається коло, що

складається з котушки з індуктивністю L і конденсатора з ємністю C.

Знайдемо рівняння коливань у контурі, в якому опір

дорівнює нулю (R = 0 ). Застосуємо закон Ома для ділянки кола

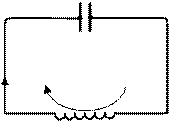
1-3-2 (див. рис. 27.1):

IR = j1- j2+ E s. (27.1)

Різницю потенціалів на конденсаторі визначимо із співвідношення

j1- j2= q 1/ C = (- q)/ C. (27.2)

C

+ q - q

2 1

I

L

Рисунок 27.1

Тут використали, що заряд пластини конденсатора 1 q 1= - q

(див. рис. 27.1).

Сила струму I є додатною, коли напрям струму співпадає з напрямом обходу ділянки

кола 1-3-2, тобто за годинниковою стрілкою. В цьому разі заряд на пластині конденсатора

q 2 = q

пов’язаний з силою струму в ділянці кола наступним співвідношенням

I = + dq / dt = + q ÿ. (27.3)

Знак «+» обумовлений тим, що, коли струм I є додатним, заряд q 2 = q

збільшується (q ÿ > 0).

Підставимо в (27.1) закон самоіндукції

E s = - L dI / dt, співвідношення (27.2) й (27.3),

умову R = 0

й отримуємо

0 = - q / C - L q ÿÿ. (27.4)

Далі, виконавши прості перетворення, прийдемо до диференціального рівняння гармонічних коливань

q ÿÿ + (1/(LC)) q = 0. (27.5)

Таким чином, заряд на обкладках конденсатора змінюється за гармонічним законом

с частотою

q = qm cos(w0 t + a)

(27.6)

w0 = 1/

LC. (27.7)

Ця частота називається власною частотою контуру. Для періоду коливань знаходимо так звану формулу Томсона:

T = 2p / w0= 2p

LC. (27.8)

Зрозуміло, що напруга на конденсаторі та сила струму в коливальному контурі також змінюються за гармонічним законом.

§ 28 Векторна діаграма. Додавання двох гармонічних коливань одного напрямку й частоти [5]

1 Розгляд багатьох питань, зокрема додавання Y декількох гармонічних коливань одного напрямку й w0однакової частоти, значно полегшується й стає

наочним, якщо зображувати коливання графічно у

вигляді векторів на площині. Схема, в якій коливання A

зображуються графічно у вигляді векторів на

площині, називається векторною діаграмою. a X

Візьмемо вісь X, уздовж якої будемо

відкладати коливальну величину x (рис. 28.1). З O x

узятої на осі точки O відкладемо вектор довжиною

A, що утворює із віссю X кут a. Якщо обертати цей

вектор з кутовою швидкістю w0

.

проекція кінця вектора A

змінюватись за законом

відносно точки O, то на вісь X буде

Рисунок 28.1 – Векторна діаграма гармонічного коливання з

x = A cos(w0 t + a). (28.1)

Таким чином, гармонічне коливання може

амплітудою A й початковою фазою

a

бути заданим за допомогою вектора, довжина якого дорівнює амплітуді коливання, а напрям утворює з віссю X кут, що дорівнює початковій фазі коливань. Схема, яка зображена на рис. 28.1, є векторною діаграмою гармонічного коливання (28.1).

2 Розглянемо додавання двох

гармонічних коливань одного напрямку й Y K. однакової частоти. Знайдемо параметри A результуючого коливання x, яке буде сумою y 1

коливань

x 1і

x 2, які визначаються функціями

x 1= A 1cos(w0 t + a1),

x 2= A 2cos(w0 t + a2). (28.2) y 2

.

A 2.

A 2

.

(a2- a1)

a1

З фізичних міркувань зрозуміло, що A 1 D

результуюче коливання M

x = x 1+ x 2

(28.3) a2 a

a

B

1

буде гармонічним коливанням з частотою

O x x 2

коливань w0

(як і коливання

x 1 та

x 2), 1 X

амплітудою A та початковою фазою a:

x = A cos(w0 t + a). (28.4)

Таким чином, задача про додавання двох гармонічних коливань одного напрямку й

x

Рисунок 28.2 – Векторне додавання двох гармонічних коливань одного напрямку й однакової частоти

однакової частоти зводиться до знаходження невідомої амплітуди A й невідомої початкової фази a результуючого коливання x.

Використаємо метод векторних діаграм. Подамо обидва коливання за допомогою

.

векторів A 1 і

.

.

A 2 (рис. 28.2). Побудуємо за правилами додавання векторів результуючий

вектор A. З рисунка випливає, що проекція цього вектора на вісь X дорівнює сумі проекцій

.

векторів, що додаються:

x = x 1+ x 2, що збігається з (28.3). Отже, вектор A

пов’язаний з

результуючим коливанням x. Цей вектор обертається з тією ж кутовою швидкістю

w0, як і

вектори

.

A 1й

.

A 2. Тобто, сума

x 1і x 2

є гармонічним коливанням із частотою w0, амплітудою

A й початковою фазою a.

Визначимо невідомі амплітуду A й початкову фазу a результуючого коливання x,

виходячи з геометричних міркувань (див. рис. 28.2). Розглянемо трикутник застосуємо теорему косинусів і одержимо

D OMK,

1 2 1 2

[ (2

1)] 1

1 2 (2

1). (28.5)

A 2= A 2+ A 2- 2 A A

cos p - a - a

= A 2 + A 2 + 2 A A

cos a - a

Тут використали, що кут

Ð OMK = p - (a2- a1). Далі позначивши через

y 1,

y 2 та

x 1, x 2

проекції векторів рис. 28.2, що

.

A 1,

.

A 2, відповідно на осі Y, X неважко знайти з трикутника

D OBK на

tg a = y 1+ y 2=

x 1+ x 2

A 1 sin a1 + A 2 sin a2

A 1cos a1+ A 2cos a2

. (28.6)

Співвідношення (28.5) та (28.6) є розв’язанням поставленої вище задачі. Таким чином, метод векторних діаграм дозволяє додавання гармонічних функцій (коливань) замінити додаванням векторів.

Формули (28.2) і (28.3) можна, звичайно, отримати із тригонометричних міркувань, розв’язавши тригонометричне рівняння

A cos(w0 t + a) = A 1cos(w0 t + a1)+ A 2cos(w0 t + a2) (x = x 1+ x 2)

відносно амплітуди A і фази a. Але графічний спосіб отримання цих формул є більш простим і наочним. Ці переваги особливо є корисними у випадку, коли доводиться складати велику кількість коливань.

§ 29 Биття [5]

1 Розглянемо випадок, коли два гармонічних коливання одного напрямку, які додаються, мало відрізняються за частотою. Процес, який при цьому виникає, можна розглядати як квазігармонічне коливання з пульсуючою амплітудою. Таке коливання називається биттям.

Позначимо частоту одного з коливань через w, частоту іншого коливання через

w + Dw. За умовою Dw << w. Амплітуди коливань будемо вважати однаковими й такими, що дорівнюють A. Щоб спростити математичні перетворення, припустимо, що початкові фази

обох коливань дорівнюють нулю. Тоді рівняння коливань будуть мати вигляд

x 1= A cos w t,

x 2= A cos[(w + Dw) t ].

Склавши ці вирази й застосувавши формулу для суми косинусів

= 2 cos((a + b) / 2)× cos(a - b) / 2), отримуємо

cos a + cosb =

1 2 ç

x = x + x = æ 2 A cos

è

Dw t ö cos w t, (29.1)

÷

2 ø

де у другому множнику ми знехтували доданком

(29.1) зображений на рис. 29.1 а.

Dw / 2

у порівнянні з w. Графік функції

T = 2p

w

x M 2

a

t

M 1 TA = 2p / Dw

Дата добавления: 2014-01-11