Фотоелектричним ефектом, або фотоефектом

називається вибивання електронів речовини під дією світла. Це

явище було відкрито Г.Герцом у 1887 р. Він помітив, що проскакування іскри між кульками розрядника значно полегшується, коли одну з кульок освітити ультрафіолетовими променями.

У 1888-1889 рр. А.Г.Столєтов провів систематичне

дослідження фотоефекту за допомогою установки, схема якої показана на рис. 73.1. Конденсатор, що утворений дротяною сіткою

G

+ –

Рисунок 73.1

й суцільною пластиною, був включений послідовно з гальванометром G у ланцюг батареї. Світло, проходячи через сітку, падало на суцільну пластину. У результаті в електричному

колі виникав струм, який реєструвався гальванометром. На базі своїх дослідів Столєтов дійшов до таких висновків: 1) найбільшу дію мають ультрафіолетові промені; 2) сила струму

зростає зі збільшенням освітленості пластини; 3) заряди, що випускаються під дією світла, мають від’ємний знак.

Через 10 років (у 1898 р.) Ленард і Томсон, вимірявши питомий заряд частинок, які

вибиваються під дією світла, встановили, що ці частинки є електронами (електрон був відкритий Томсоном у 1897 р.).

2 Ленард й інші дослідники вдосконалили прилад Столєтова, помістивши електроди в евакуйований балон (рис. 73.2). Світло, що проникає через кварцове віконце Кв, освітлює

катод К, який виготовлений з досліджуваного матеріалу. Електрони, вибиті внаслідок фотоефекту, рухаються під дією електричного поля до анода А. У результаті цього у

електричному колі приладу проходить фотострум, який вимірюється гальванометром G.

Напругу між анодом і катодом можна змінювати за допомогою потенціометра П.

Kв

I

K A Iн

V

G

П U з 0 U

– +

Рисунок 73.2 Рисунок 73.3

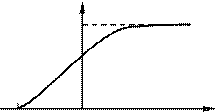
Отримана на такому приладі вольт-амперна характеристика (тобто крива залежності фотоструму I від напруги між електродами U) наведена на рис. 73.3. Зрозуміло, що вольт- амперна характеристика знімається при незмінному потоці світла F. Із цієї кривої видно, що при деякій не дуже великій напрузі фотострум досягає насичення – всі електрони, які

випущені катодом, попадають на анод. Отже, сила струму насичення

Iн визначається

кількістю електронів, які випускаються катодом за одиницю часу під дією світла.

Пологий хід кривої вказує на те, що електрони вилітають із катода з різними за

величиною швидкостями. Частина електронів, що відповідає силі струму при

U = 0, має

швидкості, які є достатніми для того, щоб долетіти до анода «самостійно», без допомоги прискорювального поля. Для того щоб сила струму стала дорівнювати нулю, потрібно

прикласти затримуючу напругу

U з. При такій напрузі жодному з електронів, який навіть

має при вильоті з катода найбільше значення швидкості

затримуюче поле й досягти анода. Тому можна написати, що

u m, не вдається перебороти

1 2

m u m = eU з, (73.1)

де m – маса електрона. Таким чином, вимірявши затримуючу напругу U з, можна визначити максимальне значення швидкості фотоелектронів.

До 1905 р. було експериментально з'ясовано, що максимальна швидкість

фотоелектронів не залежить від інтенсивності світла, а залежить тільки від його частоти –

збільшення частоти приводить до зростання швидкості. Також було визначено, що струм

насичення

Iн є пропорційним до інтенсивності світла, яке падає на поверхню

досліджуваного матеріалу.

Таким чином, дослідним шляхом були встановлені три закони фотоефекту:

1) Максимальна початкова швидкість фотоелектронів визначається частотою світла й не залежить від його інтенсивності.

2) Для кожної речовини існує червона межа фотоефекту, тобто така найменша частота світла w0, при якій ще можливий фотоефект.

3) Число фотоелектронів, що вириваються з катода за одиницю часу (струм насичення Iн), прямо пропорційне інтенсивності світла.

Установлені експериментально залежності не вкладаються в рамки класичних

уявлень. Наприклад, швидкість фотоелектронів за класичними поняттями повинна зростати з амплітудою, а, отже, і з інтенсивністю електромагнітної хвилі.

3 У 1905 р. А. Ейнштейн показав, що всі закономірності фотоефекту легко пояснюються, якщо припустити (гіпотеза Ейнштейна), що світло поглинається такими

самими порціями

hw (квантами), якими воно, за припущенням Планка, випромінюється. На

думку Ейнштейна, енергія, отримана електроном, передається йому у вигляді кванта

hw,

який ним поглинається повністю. Частина цієї енергії, яка дорівнює роботі виходу A,

витрачається на те, щоб електрон міг покинути тіло. Якщо електрон звільняється світлом не біля поверхні, а на деякій глибині, то частина енергії, яка дорівнює E ¢, може бути загублена

внаслідок випадкових зіткнень у речовині. Залишок енергії утворює кінетичну енергію Ek

електрона, який покинув речовину. Енергія Ek

буде максимальною, коли

E ¢= 0. У цьому

випадку повинне виконуватися співвідношення

1 2

hw = 2 m u m + A

яке називається формулою Ейнштейна для фотоефекту.

(73.2)

Фотоефект і робота виходу залежать від стану поверхні металу (зокрема, від окисів,

що знаходяться на ній, адсорбованих речовин). Тому довгий час не вдавалося перевірити формулу Ейнштейна з достатньою точністю. У 1916 р. Міллікен створив прилад, у якому досліджувані поверхні піддавалися очищенню у вакуумі, після чого вимірялася робота виходу й досліджувалася залежність максимальної кінетичної енергії фотоелектронів від

частоти світла (ця енергія визначалася шляхом виміру затримуючого потенціалу Результати виявилися в повній відповідності до формули (73.2).

U з).

Підставивши у формулу (73.2) виміряні значення A й

m u2/ 2

(при даній w),

m

Міллікен визначив значення сталої Планка h, яка збігалася зі значеннями, знайденими зі спектрального розподілу рівноважного теплового випромінювання й з короткохвильової межі гальмівного рентгенівського спектра.

З формули (73.2) випливає, що у випадку, коли робота виходу A перевищує енергію

кванта

hw, електрони не можуть покинути метал. Отже, для виникнення фотоефекту

необхідне виконання умови hw ³ A, або

w ³ w0= A / h. (73.3)

Відповідно для довжини хвилі маємо умову

l £ l0

= 2ph c

A

. (73.4)

Частота w0

або довжина хвилі l0

називається червоною межею фотоефекту.

Число електронів, які вивільняються внаслідок фотоефекту, повинне бути пропорційне числу падаючих на поверхню квантів світла. Разом з тим світловий потік F визначається кількістю квантів світла, що падають на поверхню за одиницю часу. Відповідно

до цього струм насичення Iн

повинен бути пропорційний падаючому світловому потоку:

Iн ~ F. (73.5)

Зазначимо, лише мала частина квантів передає свою енергію фотоелектронам. Енергія інших квантів витрачається на нагрівання речовини, яка поглинає світло.

Крім розглянутого нами вище зовнішнього фотоефекту (який називають просто фотоефектом), існує також внутрішній фотоефект, який спостерігається у діелектриках і напівпровідниках. Про нього буде йти мова пізніше.

§ 74 Фотони. Дослід Боте. Властивості фотонів. Корпускулярно-хвильовий дуалізм світла [6]

1 Щоб пояснити розподіл енергії у спектрі рівноважного теплового випромінювання,

досить, як показав Планк, припустити, що світло тільки випромінюється порціями

hw. Для

пояснення фотоефекту досить припустити, що світло поглинається такими самими порціями. Однак Ейнштейн пішов значно далі. Він висунув гіпотезу, що світло й поширюється у

вигляді дискретних частинок, які спочатку назвали світловими квантами. Потім ці квазічастинки отримали назву фотонів.

2 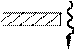Найбільш безпосереднє підтвердження гіпотези Ейнштейна дав дослід Боте. Тонка металева

фольга Ф (рис. 74.1) знаходилася між двома

опромінювалася слабким пучком рентгенівських променів, під дією яких вона сама ставала джерелом рентгенівських променів (це явище називається рентгенівською флуоресценцією). Внаслідок малої інтенсивності первинного пучка кількість квантів, що

попаданні рентгенівських променів на лічильник він спрацьовував і пускав у хід особливий механізм М, що робив відмітку на рухомій стрічці С. Якби випромінювана енергія поширювалася рівномірно в усі сторони, як це випливає із хвильових уявлень, обидва лічильники повинні були б спрацьовувати

Л Л

M M

C

Рисунок 74.1

одночасно й відмітки на стрічці знаходились б одна проти одної. У дійсності ж спостерігалося абсолютне невпорядковане розміщення відміток. Це можна пояснити лише тим, що в окремих актах випромінювання виникають світлові частинки, які летять то в одному, то в іншому напрямку.

Отже, було експериментально доведене існування особливих частинок світла –

фотонів.

3 Розглянемо властивості фотонів. Енергія фотона у відповідно до гіпотези Ейнштейна визначається його частотою:

E = hw. (74.1)

Фотон рухається з такою самою швидкістю, як і електромагнітна хвиля у вакуумі. Це означає, що швидкість фотона

u = c

дорівнює швидкості світла. Слід взяти до уваги, що фотони рухаються зі швидкістю c не тільки у вакуумі, але й у речовині. «Уповільнення» світла в речовині обумовлене тим, що при проходженні через речовину фотони поглинаються атомами й слідом за цим випромінюються знову. Між актами поглинання й випромінювання проходить деякий час, внаслідок чого середня швидкість фотонів у речовині виявляється меншою за c.

Енергія E й імпульс частинки p, як випливає зі спеціальної теорії відносності, пов’язані між собою таким виразом:

p = E u. (74.2)

c 2

Підставивши у цю формулу вираз для енергії (74.1), отримаємо для імпульсу фотона зв’язок з частотою світла

p = E c = hw. (74.3)

c 2 c

Замінивши у формулі (74.3) частоту w через довжину хвилі l, отримаємо для імпульсу фотона вираз

p = h2p= h k

l

(74.4)

(k – хвильове число). Фотон летить у напрямку поширення електромагнітної хвилі. Тому напрями імпульсу p і хвильового вектора k збігаються. Отже, формулу (74.4) можна записати у векторному вигляді:

p. = h k. (74.5)

Зі спеціальної теорії відносності також відоме співвідношення, яке пов’язує імпульс

p, повну енергію E та масу спокою m частинки:

E 2 - c 2 p 2= m 2 c 4. (74.6)

Підставимо в (74.6) формули (74.1) та (74.3) і отримаємо для маси спокою

E 2 - c 2 p 2

m = =

c 2

(hw)2- c 2(hw / c)2

c 2

= 0. (74.7)

Отже, маса спокою фотона дорівнює нулю.

При взаємодії з речовиною фотони можуть випромінюватися, поглинатися й розсіюватися. Збереження числа фотонів не має місця. Але закони збереження енергії й

імпульсу для фотонів повинні виконуватися.

Таким чином, фотон є частинкою особливого роду, яка відрізняється від таких частинок, як електрон, протон і т.п., що можуть існувати, рухаючись зі швидкостями, меншими за швидкість світла c, і навіть перебувати у стані спокою.

4 Ми розглянули ряд явищ, у яких світло веде себе як потік частинок (фотонів). Однак не слід забувати, що такі явища, як інтерференція й дифракція світла, можуть бути пояснені тільки на основі хвильових подань. Таким чином, світло виявляє корпускулярно хвильовий дуалізм (подвійність): в одних явищах проявляється його хвильова природа, і він веде себе як електромагнітна хвиля, в інших явищах проявляється корпускулярна природа світла, і він веде себе як потік фотонів. Далі ми побачимо, що корпускулярно-хвильовий дуалізм властивий не тільки квантам світла (фотонам), але й частинкам речовини (електронам, протонам, атомам і т.д.).

З'ясуємо, як пов’язані між собою хвильова й корпускулярна картина. Відповідь на це питання можна отримати, розглянувши з обох точок зору освітленість деякої поверхні. Відповідно до хвильових уявлень освітленість у деякій точці поверхні пропорційна квадрату амплітуди світлової хвилі. З корпускулярної точки зору освітленість пропорційна густині потоку фотонів. Отже, між квадратом амплітуди світлової хвилі й густиною потоку фотонів є пряма пропорційність. Таким чином, хвильові властивості світла пов’язані з кількістю фотонів, що попадають у дану точку простору. Тобто хвильові властивості світла з точки зору корпускулярних уявлень пов’язані зі статистичними властивостями потоку фотонів.

§ 75 Ефект Комптона. Зміна довжини хвилі фотона при його розсіюванні на електроні [6]

1 Особливо виразно проявляються корпускулярні властивості світла в явищі, яке отримало назву ефекту Комптона. У 1923 р. Комптон, досліджуючи розсіювання

рентгенівських променів різними речовинами, виявив, що в розсіяних променях разом з випромінюванням початкової довжини хвилі l містяться також промені більшої довжини

хвилі l¢. Різниця

Dl = l¢- l

виявилася залежною тільки від кута q між напрямками

розсіяного випромінювання та первинного пучка. Виявилось, що від довжини хвилі l й від

природи речовини, на якій відбувається розсіювання, Dl

2 Схема досліду Комптона показана на рис. 75.1.

Діафрагмами Д виділяється вузький пучок монохроматичного (характеристичного) рентгенівського випромінювання і спрямовується на розсіювальну речовину РР. Спектральний склад розсіяного випромінювання досліджується за допомогою рентгенівського спектрографа, який складається із кристала Кр й іонізаційної камери ІК.

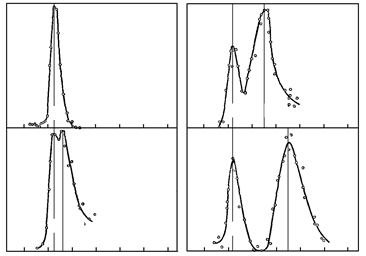
На рис. 75.2 наведені результати дослідження

розсіювання монохроматичного рентгенівського

не залежить.

Д Д

РР

q

IK Kp

випромінювання (лінія

K aмолібдену) на графіті. Крива

a характеризує первинне випромінювання. Інші криві належать до різних кутів розсіювання q, значення яких

Рисунок 75.1 – Схема досліду Комптона

подані на рисунку. Вздовж осі ординат відкладена інтенсивність випромінювання, вздовж осі

абсцис – довжина хвилі.

K aMo

а в

q = 90°

P

q = 45°

б

P M

q = 135°

г

P M P M

Рисунок 75.2 – Залежність інтенсивності розсіяного на графіті рентгенівського випромінювання від довжини хвилі

3 Усі особливості ефекту Комптона можна пояснити, розглядаючи розсіювання як

процес пружного зіткнення рентгенівських фотонів із практично вільними електронами. Вільними можна вважати електрони, які слабо зв’язані з атомами, енергія зв'язку яких значно менша від тієї енергії, яку фотон може передати електрону при зіткненні.

Нехай на вільний електрон, який у початковому стані перебуває у стані спокою, падає

фотон з енергією

hw й імпульсом h k

(рис. 75.3). Енергія електрона до зіткнення дорівнює

mc 2

(m – маса електрона), імпульс дорівнює нулю. Після зіткнення електрон буде мати

імпульс p й енергію, яка дорівнює c

p 2+ m 2 c 2

(див. відповідну формулу спеціальної теорії

відносності). Енергія й імпульс фотона також зміняться й будуть дорівнювати законів збереження енергії й імпульсу випливають дві рівності:

hw¢й

h k ¢. Із

hw + mc 2= hw¢+ c

p 2+ m 2 c 2, (75.1)

h k = p. + h k ¢

(75.2)

Розділимо першу рівність на c й напишемо її у вигляді

p 2+ m 2 c 2= h(k - k ¢) + mc

h k ¢

(w / c = k

). Піднесення до квадрата дає

q

p 2= h2(k 2 + k ¢2- 2 kk ¢) + 2h mc (k - k ¢). (75.3)

h k

З (75.2) випливає, що

p 2= h2(k - k ¢)2= h2(k 2 + k ¢2- 2 kk ¢cos q)

(75.4)

(q – кут між векторами k й k ¢, див. рис. 75.3). З порівняння виразів (75.3) і (75.4) отримуємо

mc (k - k ¢) = h kk ¢(1- cos q).

Помножимо цю рівність на 2p й розділимо на mckk ¢:

2p- 2p= 2ph(1- cos q).

p

Рисунок 75.3 – Розсіювання рентге- нівського фотона на електроні, який спочатку перебував у стані спокою: p – імпульс електрона;

k ¢ k mc

h k – імпульс фотона до зіткнення з

Нарешті, врахувавши, що

2p / k = l, прийдемо до

електроном;

h k ¢

– імпульс фотона

формули

де

Dl = l¢- l = l C (1- cos q), (75.5)

після зіткнення; q – кут розсі- ювання

l = 2ph. (75.6)

C mc

Обумовлена цим виразом величина l C

називається комптонiвською довжиною

хвилі тієї частинки, маса m якої мається на увазі. У розглянутому нами випадку l C –

комптонiвська довжина хвилі електрона. Підстановка значень h, m і c дає для l C

електрона значення

l C = 0,00243 нм. (75.7)

Результати вимірів Комптона знаходяться у повній узгодженості з формулою (75.5),

якщо підставити в неї значення (75.7) для l C.

4 При розсіюванні фотонів на електронах, зв'язок яких з атомом достатньо сильний, обмін енергією й імпульсом відбувається з атомом як цілим. Оскільки маса атома набагато перевершує масу електрона, комптонiвське зміщення у цьому випадку є дуже малим й l¢практично збігається з l. У міру зростання атомного номера збільшується відносне число електронів із сильним зв'язком, чим і обумовлюється ослаблення зміщеної лінії.

Дата добавления: 2014-01-11