Интегрирование по частям в определенном интеграле

Замена переменной в определенном интеграле

Теорема 3. Пусть дан интеграл , где f (x) – непрерывная функция на [ a, b ]. Введем новую переменную t, связанную со старой переменной соотношением x = j (t). Если выполняются условия:

1) j (a) = а, j (b) = b,

2) j (t) и j¢ (t) непрерывны на [ a, b ],

3) f [ j (t)] определена и непрерывна на [ a, b ],

то .

Пусть u и v – дифференцируемые функции от x. Тогда

(uv)¢ = u ¢ v + uv ¢

Интегрируя обе части тождества, получим: .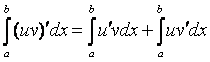

Т.к. , то ;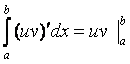

следовательно, , или окончательно .

2.4 Лекция 8. Двойные интегралы

Содержание лекции: Двойной интеграл и его свойства. Вычисление двойных интегралов в прямоугольных координатах. Замена переменных в двойном интеграле.

Цели лекции: знакомство с двойным интегралом, его свойствами и техникой вычисления.

Рассмотрим в плоскости Oxy замкнутую область D, ограниченную линией L.

Пусть в области D задана непрерывная функция z = f (x, y).

Разобьем область D произвольным образом на п частей:

D s₁, D s₂, D s₃, …, D s_п.

Каждую часть (площадку) отождествим с ее площадью.

Выберем в каждой площадке произвольную точку Р_i Î D s_i (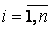), и сопоставим ей значение f (P_i). Составим сумму: .

Эта сумма называется интегральной суммой для функции f (x, y) в области D.

Если f ³ 0 в области D, то геометрически каждое слагаемое f (P_i) D s_i можно представить как объем малого цилиндра, высота которого есть f (P_i), а основание D s_i.

Таким образом, V_n – объем «ступенчатого» тела. Предположим, что diam D s_i ® 0 при n ® ¥. Тогда справедлива следующая теорема.

Теорема 1. Если функция f (x, y) непрерывна в замкнутой области D, то .

Этот предел не зависит ни от способа разбиения области D на D s_i , ни от выбора точки Р_i Î D s_i.

Этот предел называется двойным интегралом от функции f (x, y) в области D и обозначается: или .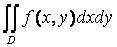

Таким образом, ,

где D – область интегрирования.

Геометрический смысл двойного интеграла ( в случае f (x, y) ³ 0):двойной интеграл равен объему тела V, ограниченного поверхностью z = f (x, y), плоскостью z = 0 и цилиндрической поверхностью с образующей, параллельной оси Оz и направляющей L.

Свойства двойного интеграла:

1) ;

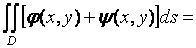
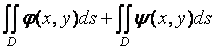2) 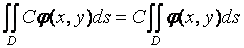, С = const;

3) Если D разбита на D₁ и D₂ без общих внутренних точек, то

.

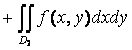Дата добавления: 2014-01-11