Прибуток є максимальним в точці, де граничний дохід рівний граничним витратам

Приклад 11. Розглянемо умови прикладу 10. Прирівняємо граничні витрати та граничний дохід і отримаємо

МR(x)=МC(x),

1500x=2x,

x=750.

Отже, при таких умовах фірма може отримати найбільший прибуток P(750)=1500*750-750²-500000=$62500. Перевіримо, що виготовляючи та продаючи 800 одиниць продукції, фірма отримає менший прибуток P(800)=1500*800-800²-500 000=$60 000<$62 500.

Що робити, якщо фірма ще не визначила ціну на свою продукцію. Для фірми ціна, яку вона мусить визначити, щоб отримати певний дохід, залежить від попиту на цю продукцію. Якщо попит є великим, то фірма може продавати велику кількість одиниць по низькій ціні. Якщо попит на продукцію малий, то фірма не може продавати багато одиниць продукції і тому вона встановлює вищу ціну, щоб отримати той самий дохід. Якщо через p позначити ціну одиниці продукції, а x кількість, на яку є попит, то залежність p від x задає функція попиту p=d(x). Тоді дохід фірми від продажу x одиниць продукції буде становити

R(x)=xp=xd(x).

Похідну часто використовують для визначення еластичності попиту. Розглянемо типову функцію попиту q=d(p), де p позначає ціну одиниці продукції, q – кількість продукції, на яку є попит. Похідна q^’=d^’(p) показує показник зміни попиту відносно ціни. Якщо úd^’(p)ú є великим, то попит різко падає при зростанні ціни. Якщо úd^’(p)ú є малим, то попит повільно падає при зростанні ціни.

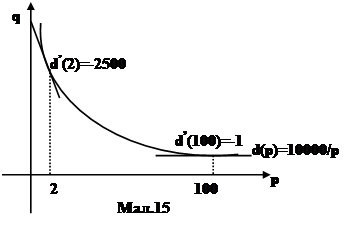Приклад 12. Нехай функція попиту задана рівнянням d(p)=10000/p. Тоді d^’(p)=-10000/p².

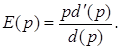З мал.15 видно, що коли ціна є $2, то мале зростання ціни призводить до значного падіння попиту (фактично, коли ціна $2, то зростання ціни на $1 призводить до падіння попиту приблизно на ú d^’(2)ú=2500 одиниць). З іншої сторони, коли ціна є $100, то мале зростання ціни призводить лише до малого падіння попиту (зростання на $1 ціни призводить в цьому випадку до падіння попиту всього на úd^’(p)ú=1 одиницю). Коли мала зміна ціни призводить до великої зміни попиту, то кажуть, що попит є еластичним. Коли мала зміна ціни призводить до малої зміни попиту, то говорять, що попит є нееластичним. Якщо функція попиту на товар визначається рівнянням q=d(p), то коефіцієнт еластичності попиту на товар за ціною p визначається формулою

Коефіцієнт еластичності вимірює відношення відносної похибки зміни попиту до відносної похибки зміни ціни. Якщо ú E(p)ú>1, то попит є еластичним, якщо úE(p)ú<1, то попит є нееластичним. Якщо úE(p)ú=1, то попит є одиничної еластичності. Одинична еластичність означає, що мала зміна ціни призводить до незначної зміни попиту, що дохід залишається приблизно незмінним.

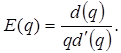Тут ми розглядали попит, як функцію залежності кількості від ціни. Економісти часто визначають попит, як функцію залежності ціни від кількості. В цьому випадку функція попиту задається рівнянням p=d(q) і коефіцієнт еластичності обчислюємо за формулою

Приклад 13. Якщо функція попиту на товар задана рівнянням

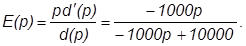q=-1000p+10 000,

то коефіцієнт еластичності попиту дорівнює

Припустимо, що p=$2. Тоді

úE(p)ú=úE(2)ú=ú-0,25ú=0,25<1,

тому попит на товар є нееластичним при ціні $2. Зауважимо, що коли p=$2, то кількість, на яку є попит рівна q=8000 одиниць і дохід дорівнює $2*8000=$16000. Якщо ціна зросте на 10% до $2,20, то попит впаде до 7800 і дохід зросте до $2,20*7800=$17160. Отже, коли ціна рівна $2, то зростання ціни на 10% призводить до малого падіння попиту та зростання доходу.

Нехай ціна p=$8. Тоді

úE(p)ú=úE(8)ú=ú-4ú=4>1,

тому попит на товар є еластичним. Коли p=$8, то попит рівний q=2000 одиниць і дохід дорівнює $8*2000=16000 знову. Але тепер зростання ціни на 10%, з $8 до $8,80, призведе до падіння попиту до 1200 одиниць і падіння доходу до $10560. Тому, коли p=$8, то зростання ціни на 10% веде до великого падіння попиту і великого падіння доходу. Отже, в цьому випадку потрібно опускати ціни, що призведе до значного зростання попиту та зростання доходу.

Коли úE(p)ú=1, наприклад при ціні p=$5, то зростання (падіння) ціни призводить до незначного падіння (зростання) попиту, але дохід при цьому залишається приблизно однаковим.

Найчастіше похідну використовують при дослідженні функції на екстремум. Припустимо, що функція має графік, зображений на мал.16.

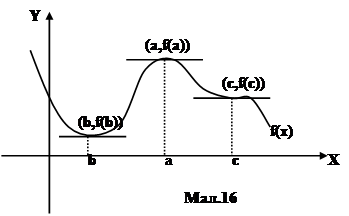Зауважимо, що функція в точці x=a має пік, а в точці x=b – дно. Точку (a,f(a)) називають локальним максимумом, а точку (b,f(b)) - локальним мінімумом. Точку x=a називають точкою локального максимума, якщо для довільних точок x<a і x>a функція приймає значення f(x)<f(a). Точку x=b називають точкою локального мінімума, якщо для довільних значень x<b і x>b функція приймає значення f(x)>f(b). Зауважимо, що в точках x=a та x=b функція не змінює свого значення. Отже, похідна функції в цих точках дорівнює нулю. Якщо f позначає функцію, то точку x=a називають критичною, якщо f ^’ (a)=0 або f ^’(a) не існує.

Тепер розглянемо зв’язок знака похідної та поведінки функції. Припустимо, що похідна функції f в точці x=a є додатня, тобто f ^’ (a)>0. Тоді кожне зростання аргумента на 1 одиницю призводить до зростання значення функції на f ^’(a) одиниць. Отже, функція зростає. Подібний висновок робимо, якщо похідна приймає значення f ^’(a)<0. В цьому випадку зростання аргумента на 1 одиницю призводить до падіння значення функції на f ^’(a) одиниць. Отже, функція спадає. Тому, маємо наступний висновок про

зв’язок знака похідної та поведінки функції

- якщо f ^’(x)>0 для всіх x з проміжка (с,d), то функція зростає на цьому проміжку,

- якщо f ^’(x)<0 для всіх x з проміжка (c,d), то функція спадає на цьому проміжку.

Повернемося до поняття критичних точок. Якщо для деякої функції ми визначили критичну точку, то треба перевірити чи є вона точкою максимума, чи точкою мінімума, чи не є точкою екстремума. Припустимо, що x=a є критичною точкою для f і f ^’(x)>0 коли x з проміжка (c,а), а f ^’(x)<0 коли x з проміжка (a,b). Отже, зліва від x=a функція зростає, а справа від x=a функція спадає. Тому, як видно з мал.17, точка x=a є точкою локального максимума і максимальне значення функції дорівнює f(a).

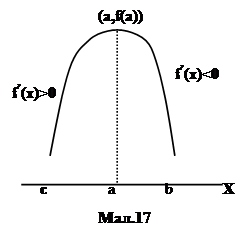Подібно мал.18 показує, якщо на проміжку (c,a) похідна f ^’(x)<0, а на проміжку (a,b) похідна f ^’(x)>0, то точка x=a є точкою локального мінімума і мінімальне значення функції дорівнює f(a). Отже, визначимо

Дата добавления: 2014-01-11