Процедуру знаходження локального екстремума

- знаходимо критичні точки функції f(x). Це ті значення x, для яких

f ^’(x)=0 або f ^’ (x) не існує

- відкладаємо критичні точки на осі x, які поділять вісь на проміжки

- визначаємо знак похідної на кожному з проміжків

а) якщо при переході через критичну точку x=a похідна змінює знак з “+” на “-“, то дана точка є точкою локального максимума

б) якщо при переході через критичну точку x=a похідна змінює знак з “-” на “+“, то дана точка є точкою локального мінімума

в) якщо при переході через критичну точку x=a похідна не змінює знак, то дана точка не є точкою екстремума

Приклад 14. Дослідимо на локальний екстремум функцію f(x)=2x³-12x²+18x+1. Користуючись визначеною процедурою, знайдемо спочатку похідну функції і вона дорівнює f ^’(x)=6x²-24x+18. Оскільки похідна всюди існує, то для знаходження критичних точок прирівняємо похідну до нуля (6x²-24x+18=0) і, розв’язавши отримане рівняння маємо, що критичними точками для даної функції є x=1 та x=3. Позначимо ці точки на осі x і визначимо знак похідної на кожному з утворених проміжків.

Розподіл знаків похідної на проміжках показано на мал.19. Використовуючи третій пункт процедури визначаємо, що точка x=1 є точкою локального максимума, а точка x=3 є точкою локального мінімума. Тому найбільше значення функція приймає f(1)=2*1³-12*1²+18*1+1=9, а найменше – f(3)=2*3³-12*3²+18*3+1=1.

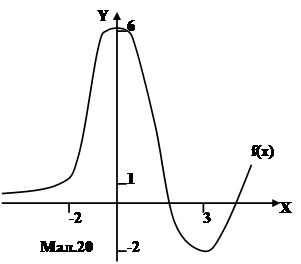Найбільше значення функції, яке вона приймає на проміжку, називають абсолютним максимумомфункції на цьому проміжку, а найменше значення функції на проміжку називають абсолютним мінімумом функції на цьому проміжку. Існування значення абсолютного максимума та абсолютного мінімума функції залежить не лише від самої функції, але і від інтервала, на якому розглядається функція. Для прикладу, розглянемо функцію f, графік якої зображено на мал.20.

- на всій осі x функція має абсолютний мінімум –2 в точці x=3, але f не має абсолютного максимума, бо права вітка функції необмежено зростає

- на проміжку [-1,4] f має абсолютний мінімум –2 в точці x=3 і абсолютний максимум 6 в точці x=0

- на проміжку [-2,1] f має абсолютний мінімум 1 в точці x=-2 і абсолютний максимум 6 в точці x=0

Як видно з мал.20, абсолютний максимум чи мінімум на проміжку може існувати, а може не існувати. Але якщо вони існують, то співпадають з локальними максимумами чи мінімумами, або рівні значенню функції на кінцях проміжка. Тому, для знаходження абсолютного екстремума потрібно знайти локальний екстремум та значення функції на кінцях проміжка. Отже, визначена

Дата добавления: 2014-01-11