Диаграмма разброса

Диаграмма разброса применяется для исследования зависимости (корреляции) между двумя видами данных. Поэтому ее называют еще полем корреляции. Диаграмма разброса используется также для выявления причинно-следственных связей показателей качества и влияющих факторов при анализе причинно-следственной диаграммы.

Например, с помощью диаграммы разброса удобно наблюдать характер изменения ПКИ во времени при воздействии тех или иных факторов. В этом случае по оси абсцисс откладываются начальные значения изучаемого ПКИ или параметров, его характеризующих: например, время осаждения химической меди перед этапом гальванического меднения. В результате будем иметь ряд значений, характеризующих начальное значение ПКИ, т.е. толщину осажденной меди. Можно было бы измерить и нанести непосредственное значение толщины покрытия, что сделать намного сложнее.

Замерив толщину слоя меди у тех же плат через некоторое время Т получим ряд значений, которые нанесем по оси ординат для каждой платы. Получим примерно такую картину:

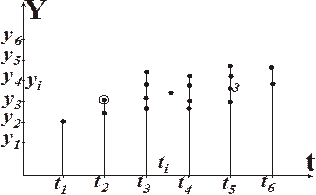
Пара значений (t_i, y_i) для каждой ПП будет отображаться точкой в системе выбранных координат, а все n точек образуют диаграмму разброса (или поле корреляции).

Если разброс параметров очень большой (несколько порядков), то удобно применять логарифмический масштаб по одной или обеим осям. Если в одну и ту же точку попадают несколько значений параметра, то эти точки выделяют, например, обводя кругами или ставя рядом числа.

Для того, чтобы проанализировать диаграмму и сделать правильные выводы, ее строят специальным образом. Сначала определяют разброс параметров по осям Dх (Dt в нашем случае) и Dу:

Dх = x_max – x_min;

Dу = y_max – y_min.

Если Dу» 0, то связь между параметрами отсутствует или эксперимент поставлен неудачно.

Далее выбирают длину осей по размерам листа бумаги. Длина осей должна быть примерно равна между собой.

Определяют масштаб (m_x = Dx / l_x; m_y = Dy / l_y) и отмечают координаты. Количество координат по осям роли не играет.

После того как на диаграмму нанесли точки, проводят исследование.

Для этого из начала координат проводят биссектрису. Если все точки лягут на биссектрису, то это значит, что рассматриваемый фактор (в нашем случае толщина слоя химической меди) связан с выходным параметром жесткой функциональной связью.

Расположение большинства точек выше или ниже биссектрисы свидетельствует о наличии корреляционной связи.

Проведя из начала координат лучи, соответствующие изменению параметра на ±10%, ±20% и т.д. можно, подсчитав количество точек, лежащих между лучами, определить частоту изменения ПКИ на соответствующую величину:

+20% – 2 точки; – 20% – 3 точки;

+40% – 6 (+ 2) точек; – 40% – 4 (+ 1) точки.

С помощью диаграммы разброса можно сравнительно быстро выяснить, имеется ли между двумя рассматриваемыми параметрами х и у корреляционная взаимосвязь, насколько она сильна и, построив методом наименьших квадратов прямую (или кривую), определить вид этой связи.

Графически различные виды корреляции можно изобразить так:

Прямая корреляция Легкая прямая Обратная (отрицательная)

корреляция корреляция

Легкая обратная Отсутствие Криволинейная

корреляция корреляции корреляция

Для того, чтобы четко определить корреляционную зависимость между параметрами и, тем более, построить прямую регрессии, необходимо получить не менее 25 пар данных. А получив формульную запись регрессии, можно, изменяя параметр х управлять изменением параметра у.

Очевидно, такое управление достаточно эффективно в случаях а) и в). В случаях б) и г) можно также управлять параметром у, но при этом необходимо также иметь в виду, что на ТП влияют и другие факторы и, может быть, не только случайные.

В случае д) никакой выраженной зависимости между х и у не наблюдается. В этом случае необходимо продолжить поиск факторов, коррелирующих с у, исключив из рассмотрения фактор х.

Если между параметрами наблюдается криволинейная зависимость, то диаграмму разброса обычно делят на участки, имеющие прямолинейный характер, и исследуют каждый участок в отдельности, как прямолинейную корреляцию.

Степень корреляционной связи х и у может быть оценена либо с помощью коэффициента корреляции (для прямолинейной корреляции), либо с помощью корреляционного отношения (для криволинейной корреляции).

Однако на практике часто применяют более простой метод оценки степени корреляционной связи – метод медиан, который заключается в следующем.

Предположим, что по таблице, связывающей пары параметров (х_i, у_i) построена диаграмма разброса.

1) Проводим вертикальную (х = х_m) и горизонтальную (у = у_m) линии на диаграмме таким образом, чтобы выше и ниже горизонтальной линии, а также справа и слева от вертикальной лежали одинаковое число точек. Линии можно при необходимости проводить и через точки. Эти линии называются медианами.

2) В каждом из четырех прямоугольников подсчитываем количество точек, которые не лежат на медианах:

n₁ = 8; n₂ = 2; n₃ = 9; n₄ = 2.

3) Складываем точки, лежащие в противоположных прямоугольниках и получаем кодовые числа:

n₍₊₎ = n₁ + n₃ = 8 + 9 = 17;

n_(-) = n₂ + n₄ = 2 + 2 = 4, (n₍₊₎ и n_(-) – кодовые числа)

n¢ = n₍₊₎ + n_(-) = 17 + 4 = 21.

Так как четыре точки лежат на медианах, то n¢ ¹ 25.

4) Используя специальную таблицу кодовых значений с определенным риском b = 0,01 или b = 0,05 по значениям n¢ и min(n₍₊₎,n_(-)) устанавливаем, существует ли корреляционная зависимость между параметрами. Для нашего случая для n¢ = 21 с вероятностью 99% (b = 0,01) n_табл =4.

У нас min(n₍₊₎,n_(-)) = n_(-)= 4.

Так как меньшее из кодовых чисел n_(-)= 4 £ n_табл, то с вероятностью 99% корреляционная зависимость существует. Если бы неравенство не выполнилось, то можно было бы проверить наличие корреляции с меньшей вероятностью.

Далее, так как n₍₊₎ >n_(-), корреляция прямая. Если бы n₍₊₎ <n_(-), то корреляция была бы обратной.

Иногда корреляцию можно установить при сдвиге параметров друг относительно друга во времени. Рассмотрим этот случай на примере.

Пример. Предположим, что фирма в течение года ежемесячно выпускает х_i единиц однотипных изделий, на некоторые из которых через какой-то срок приходят рекламации. Количество рекламаций – у_i:

xi	105	102	100	108	112	115	118	116	120	125	125	128
yi	68	71	69	66	65	70	75	76	78	77	79	82

Если ряды Х и Y упорядочить, то несложно найти медианы:

Me_у =(71 + 75)/2; Me_x = (115 + 116)/2 = 115,5.

Построим диаграмму разброса и проведем медианы:

Подсчитаем кодовые числа:

n₍₊₎ = n₁ + n₃ = 6 + 6 = 12;

n_(-) = n₂ + n₄ = 0 + 0 = 0;

n¢ = n₍₊₎ + n_(-) = 12.

Из таблицы для n¢ = 12 и b = 0,01n_табл =1.

У нас n_(-) = 0 < n_табл, следовательно, корреляция существует. Так как n₍₊₎ >n_(-), корреляция прямая.

Найдем коэффициент корреляции:

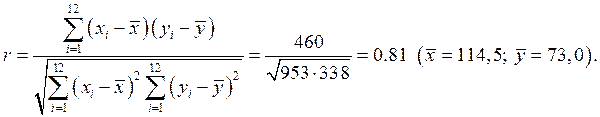
r близок к 1, следовательно, корреляция довольно высокая, т.е. х_i соответствуют значения y_i.

Сместим это соответствие на один месяц, т.е. найдем корреляционную зависимость между х₁ и у₂, х₂ и у₃, и т.д., т.е. между х_i и y_i+1, i= 1, 2, …, 11:

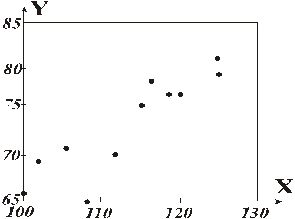
Подобный сдвиг называют временным лагом. Таким образом, мы получили диаграмму с временным лагом в 1 месяц.

Построим аналогичные диаграммы с временными лагами в 2 и 3 месяца:

Лаг на 2 месяца Лаг на 3 месяца

Рассматривая построенные диаграммы, можно сразу определить, что наиболее строгая корреляция наблюдается на диаграмме с временным лагом в 2 месяца. По-видимому, этот срок соответствует времени установки аппаратуры у покупателя, выходу ее из строя и времени пересылки рекламации. На остальных диаграммах корреляция слабее, особенно на последней.

Применяя временной лаг, можно прогнозировать поведение процесса в будущем. Определим, например, число рекламаций в 13-м месяце для временного лага в 2 месяца:

Для нашего примера:

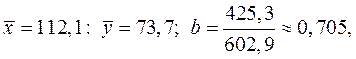
т.е. прямая регрессии будет иметь вид:

у = 73,7 + 0,705 (х – 112,1)

Если для случайных величин Х и У известны их дисперсии s²(x) и s²(y), то можно коэффициент регрессии b выразить через коэффициент корреляции r:

Определим у₁₃:

у₁₃ = 73,7 + 0,705´(125 – 112,1) = 82,79» 83.

наличия корреляции с меньшей достоверностью (н/р 95%).

Иногда корреляцию можно установить при сдвиге параметров друг относительно друга во времени.

Пример: предположим, что фирма выпускает какое-то оборудование. Объем выпуска по месяцам (хi) указан в таблице. На свое оборудование фирма ежемесячно получает рекламации, число которых также приведено в таблице.

Упорядочив хi и уi, получаем. Построим диаграмму разброса.

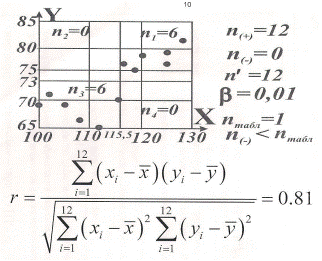
Оценим степень корреляции с помощью коэффициента корреляции. Коэффициент корреляции близок к 1, т.е. корреляция высока.

Попытаемся определить более точно, как связано количество поступаемых рекламаций с объемом выпуска продукции. Для этого сместим значения таблицы на 1 месяц (на 1 шаг), т.е. попытаемся установить взаимосвязь х1 с у2, х2 с у3 и т.д. Подобное смещение носит название временного лага. Для полученной таблицы диаграмма разброса будет иметь следующий вид:

Дальнейшее смещение приводит к ослаблению корреляции. На основании построенных диаграмм можно сделать следующий вывод: наиболее сильная корреляция наблюдается между данными, сдвинутыми на 2 месяца. По видимому, этот срок необходим покупателю на установку оборудования, её проверку, выход её из строя и пересылку рекламации.

Подобный процесс позволяет прогнозировать различные процессы. Для рассмотренного примера можно определить количество рекламаций, которые получит фирма в 13-м месяце. Для этого найдем уравнение регрессии.

Дата добавления: 2014-01-11