Уравнение прямой на плоскости. Прямая в пространстве

Определение. Уравнением линии (кривой) на плоскости Oxy называется уравнение F(x,y) с двумя переменными, которому удовлетворяют координаты x и y каждой точки данной линии и не удовлетворяют координаты любой точки, не лежащей на этой линии.

Задача о нахождении точек пересечения двух линий, заданных уравнениями F₁(x,y)=0 и F₂(x,y)=0, сводится к решению системы двух уравнений с двумя неизвестными: 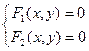. Если эта система не имеет действительных решений, то линии не пересекаются.

Простейшей из линий является прямая. Разным способам задания прямой соответствует в прямоугольной системе координат разные виды её уравнений.

Уравнение прямой с угловым коэффициентом: y=kx+b, где число k называется угловым коэффициентом, а число b- свободным членом.

Угловой коэффициент k равен тангенсу угла a наклона графика к горизонтальному направлению - положительному направлению оси Ox.

Рис. 7.1. График линейной функции - прямая

Рассмотрим частные случаи уравнения.

1. если b=0, то y=kx - уравнение прямой, проходящей через начало координат и образующей при k=tga>0 - острый угол a с осью Ox, а при k=tga<0 - тупой угол
2. если a=0, то k=tga=0, уравнение прямой, параллельной оси Ox, имеет вид y=b
3. если a=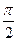, то уравнение y=kx+b теряет смысл, т. к. для неё угловой коэффициент k= tga= tg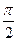не существует и уравнение имеет вид: x=a, где а - абсцисса точки пересечения прямой с осью Ox.

Уравнение пучка прямых, проходящих через точку М( 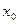, ): y-=k(x-).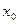

Уравнение прямой, проходящей через две данные точки: 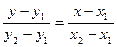, где т.М₁() и т.М₂().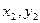

Уравнение прямой в отрезках: 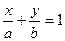, где числа a и b указывают, какие отрезки отсекает прямая на осях координат.

Общее уравнение прямой: Ax+By+C=0, где А, В, С- произвольные числа, причем А и В одновременно не равны нулю.

Рассмотрим частные случаи общего уравнения прямой:

1. если А=0, то y= -- уравнение прямой, параллельно оси Ox
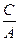2. если В=0, то y= -- уравнение прямой, параллельно оси Oy
3. если С=0, то Ax+By=0 -уравнение прямой, проходящей через начало координат.

Угол между двумя прямыми: tga=, где - угловые коэффициенты данных прямых. Если , то прямые параллельны, если 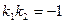, то прямые перпендикулярны.

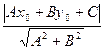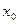Расстояние от точки до прямой: d=, где ,-координаты данной точки, а А, В, С - коэффициенты в уравнении прямой Ax+By+C=0.

Пример 7.1

Найти расстояние от точки М₀(2;-1) до прямой 3x+4y-22=0.

Решение.

d=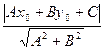==4.

Ответ: d=4.

Определение. Уравнение плоскости, записанное в виде Ax+By+Cz+D=0 называется общим уравнением плоскости.

Условие параллельности двух плоскостей: .

Условие перпендикулярности двух плоскостей: .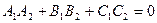

Прямая в пространстве может быть задана как линия пересечения двух плоскостей, т.е. как множество точек, удовлетворяющих системе:

.

Каноническое уравнение прямой в пространстве: еслипрямаяпараллельна направляющему вектору и проходит через точку 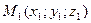, то её уравнение имеет вид: .

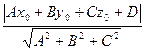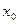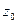Расстояние от точки до плоскости: d=, где ,,-координаты данной точки, а А, В, С, D - коэффициенты в уравнении прямой Ax+By+Cz+D=0.

Дата добавления: 2014-01-11