Из определения вычета следует

Вычисление интегралов с помощью вычетов

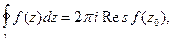(1)

т.е, зная вычет функции в точке 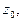мы можем вычислить интеграл по замкнутому контуру, содержащему внутри себя только одну изолированную особую точку .

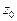Теорема 1 (основная теорема о вычетах). Если функция аналитическая всюду в ограниченной односвязной области 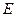за исключением конечного числа изолированных особых точек однозначного характера, то

(2)

где 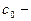замкнутая кривая, содержащая внутри все особые точки.

Доказательство. Выделим каждую особую точку замкнутым контуром 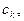содержащим только одну особую точку и воспользуемся теоремой 2 §6. В результате получим

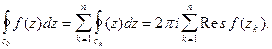
Теорема доказана.

Следствие. Если функция f (z) аналитическая во всей расширенной комплексной плоскости за исключением конечного числа особых точек, то сумма всех вычетов функции f (z), включая и вычет в точке z = ¥, равна нулю, т. е.

(3)

Здесь z_k – конечные особые точки.

Доказательство. Пусть z = R ¹ ¥ - окружность, внутри которой расположены все особые точки z_k. Тогда согласно теореме 1

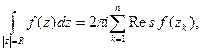(4)

где окружность z = R обходится против стрелки часов. Однако, если ее обходить по стрелке часов, то согласно определению вычета в бесконечно удаленной точке имеем

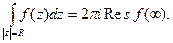(5)

Подставляя (5) (с противоположным знаком) в (4), получим 3. Следствие доказано.

Пример 1. Вычислить интеграл

Решение. Особая точка 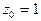лежит внутри контура 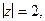поэтому, согласно (1) или (2), получим 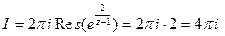(см.(2) §8).

Пример 2. Вычислить интеграл

Решение. Согласно теореме 1

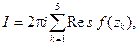
где f (z) – подынтегральная функция, а 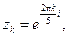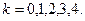Т. к. суммирование вычетов приводит к довольно громоздким вычислениям, то воспользуемся следствием теоремы 1. Получим

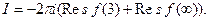
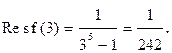
Поскольку 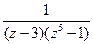~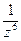при z ® ¥, то с_-1 = - Res f (¥) = 0. Итак,

При вычислении контурных интегралов от однозначной ветви многозначной аналитической функции нужно следить за тем, чтобы вычеты брались от нужной ветви.

Пример 3. Вычислить интеграл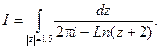

Дата добавления: 2014-01-11