Решение. В круге ½z½< 1,5 можно выделить однозначную ветвь функции Ln(z + 2)

В круге ½ z ½< 1,5 можно выделить однозначную ветвь функции Ln (z + 2). Таких ветвей бесконечное множество и они задаются формулой

Ln (z + 2) = ln½z + 2½ + iarg (z + 2) + 2 p ki, k Î Z.

Приравнивая знаменатель подынтегральной функции к нулю, получим

ln(z + 2) + iarg ½ z + 2½ + 2 p ki = 2 p i Þ z ₀ = -1, k = 1.

Таким образом, если взять ту ветвь, которая в точке z ₀ = -1 равна 2 p i, то подынтегральная функция будет иметь простой полюс в точке z ₀ = -1. Согласно (1) получим

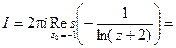
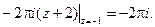
Все остальные ветви (при k ¹ 1) являются аналитическими функциями в круге ½ z ½< 1,5, поэтому I = 0.

Определенный интеграл 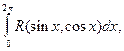где 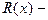дробно рациональная функция, с помощью замены сводится к интегралу по замкнутому контуру от функции комплексного переменного, который можно вычислить с помощью вычетов.

Пример 4. Вычислить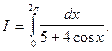

Решение.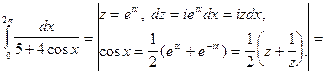

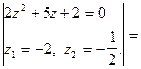
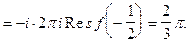
Рассмотрим вычисление несобственного интеграла

Лемма 1. Пусть функция аналитическая в верхней полуплоскости 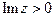всюду за исключением конечного числа изолированных особых точек. Если в точке 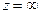функция имеет нуль не ниже второго порядка, то

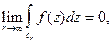
(6)

где 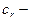верхняя часть окружности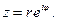

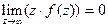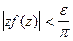Доказательство. Очевидно, или при 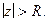На окружности 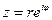получим 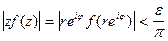при 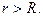Оценим интеграл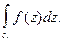

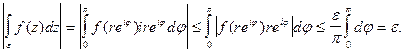
Итак, 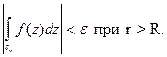Это означает, что (6) выполняется, и лемма доказана.

Теорема 2. Если функция удовлетворяет условиям леммы1, то главное значение несобственного интеграла можно найти по формуле

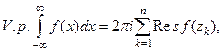(7)

где 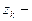особые точки в верхней полуплоскости.

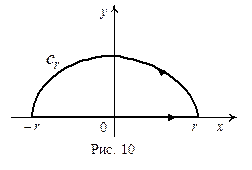
Доказательство: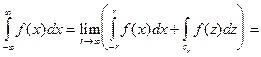

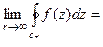
(см. рис. 10).

Воспользовались леммой 1 и теоремой 1. Теорема доказана.

Замечание. Если функция имеет только простые полюса на действительной оси, то к вычетам (7) следует добавить вычеты в этих полюсах, уменьшенные в два раза.

Пример 5. Вычислить интеграл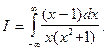

Дата добавления: 2014-01-11