Решение. Рассмотрим функцию комплексного переменного которая на действительной оси совпадает с подынтегральной функцией

Рассмотрим функцию комплексного переменного 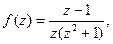которая на действительной оси совпадает с подынтегральной функцией. Она называется аналитическим продолжением функции f (x) с действительной оси на комплексную плоскость. Функция f (z) удовлетворяет лемме 1, поэтому согласно (7) и замечанию, получим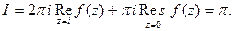

Лемма 2 (Жордан). Пусть функция является аналитической во всей комплексной плоскости за исключением конечного числа изолированных точек и равномерно относительно стремится к нулю при 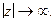Тогда

(8)

Здесь 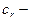верхняя часть окружности если 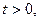и нижняя, если (без доказательства).

Теорема 3. Если функция удовлетворяет лемме 2, то

(9)

Знак плюс в (9) берется, если 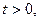а особые точки в верхней полуплоскости. Знак минус - если 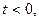а в нижней полуплоскости.

Доказать теорему 3 самостоятельно, см. доказательство теоремы 2.

Замечание к теореме 2 справедливо и для теоремы 3.

Пример 6. Вычислить

Решение.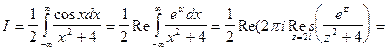

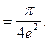
Лемма 3 (Жордан). Если функция аналитическая во всей комплексной плоскости за исключением конечного числа изолированных точек и равномерно относительно стремится к нулю при то

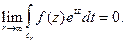(10)

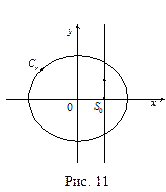
Здесь 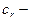часть окружности для точек которой выполняется неравенство 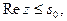если 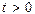(см. рис. 11). Если 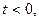то 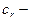другая часть этой же окружности, для точек которой 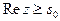(без доказательства).

Лемма 3 дает возможность вычислять с помощью вычетов несобственные интегралы вида 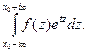(11)

Пример 7. Вычислить интеграл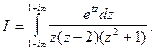

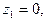
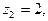
Решение. Функция удовлетворяет лемме 3. Точки 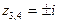являются полюсами этой функции. Пусть

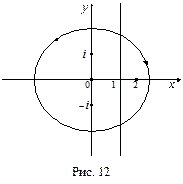
Тогда, замыкая контур интегрирования влево (см. рис. 12) и пользуясь основной теоремой о вычетах, получим

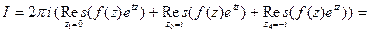
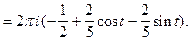
При контур интегрирования замыкаем вправо. В результате получим

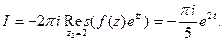
Итак,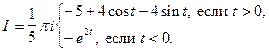

Пример 8. Вычислить интеграл

Решение. Заметим, что подынтегральная функция неоднозначная, но в правой полуплоскости можно выделить ее однозначную ветвь. Поэтому при t < 0, замыкая контур интегрирования вправо (см. рис.13) и пользуясь леммой 3, получим I = 0.

Левая полуплоскость содержит точку ветвления z₀ = -1 и в ней можно выделить однозначную ветвь подынтегральной функции, если сделать разрез от точки z₀ = -1 до бесконечности. (Положим, например, что аргумент значения 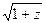на верхнем берегу разреза равен p/2. Тогда на нижнем он будет равным -p/2). Отсюда ясно, что непосредственно воспользоваться леммой 3 при t > 0 мы не можем. Поэтому рассмотрим интеграл по замкнутому контуру, расположенному в левой полуплоскости и состоящему из шести частей, из которых с ₁, с ₃ и с ₅ – отрезки прямых, с ₂ и с ₆ – части окружности радиуса R с центром в нуле, а с ₄ – окружность радиуса r с центром в точке z₀ = -1 (см. рис. 13).

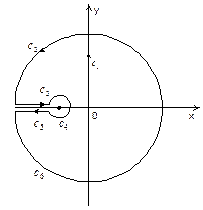
Рис.13

Внутри этого контура подынтегральная функция всюду аналитическая, поэтому интеграл равен нулю, т.е.

Согласно лемме 3 интегралы по контурам с ₂ и с ₆ при R ®¥ стремятся к нулю. Легко показать, что интеграл по контуру с ₄ при r ®0 также стремится к нулю, а интегралы по с ₃ и с ₅ противоположны по знаку. Таким образом, в пределе (R ®¥, r®0) получим

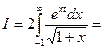
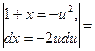
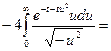
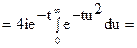
Воспользовались интегралом Пуассона (см. §3, гл.9, ч.1).

Таким образом,

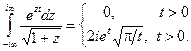
Дата добавления: 2014-01-11