Уравнение неразрывности

ЛЕКЦИЯ 6

В поле течения жидкости выделим контрольный объем V, ограниченный замкнутой поверхностью S. Сквозь этот объем протекает жидкость, перенося свои физические характеристики – массу, энергию, количество движения и т. п. Контрольная поверхность может частично состоять из физических границ, например из твердых стенок (рис.4.1). Определим массу вещества, проносимого в

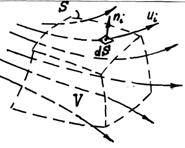Рис.4.1

единицу времени через контрольную поверхность. Для этого всю контрольную поверхность разобьем на элементарные площадки и рассмотрим элементарную площадку nidS, где ni – единичный вектор, направленный по нормали к площадке; положительным направлением считается направление наружу из объема

V. Перенос вещества через поверхность определяет нормальная составляющая скорости u_n, которая вычисляется как скалярное произведение векторов скорости и внешней нормали

u_n=u_i×n_i=u× 1× cos(u_i,n_i).

Если угол между вектором скорости и вектором внешней нормали острый, то скалярное произведение u_i×n_i положительно и, следовательно, вещество выносится через рассматриваемую площадку. Если же угол между вектором скорости и внешней нормалью к поверхности тупой, то скалярное произведение u_i×n_i будет отрицательным (косинус тупого угла <0); это значит, что через площадку dS жидкость втекает в контрольный объем. Объем жидкости, пронесенный за единицу времени через площадку dS, равен dQ=u_n×dS=u_i×n_idS, а масса жидкости, содержащаяся в этом проносимом объеме, будет равна dG=rdQ=r u_i×n_idS; это масса жидкости, перенесенная через площадку dS за единицу времени. Просуммируем теперь потоки массы, переносимые через элементарные площадки. Такое суммирование бесконечно малых потоков осуществляется интегрированием по контрольной поверхности S:

.

Величина G представляет собой массу жидкости, перенесенную за единицу времени через поверхность S; она называется массовым расходом и имеет размерность кг/с. Массовый расход через замкнутую поверхность равен разности расходов жидкости вытекающей из контрольного объема и втекающей в него. Если эта разность не равна нулю, то масса жидкости в контрольном объеме будет изменяться, и изменение массы в объеме неизменных размеров, может происходить только за счет изменения плотности жидкости. Скорость увеличения массы жидкости в контрольном объеме может быть вычислена интегралом по объему

.

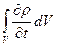Поскольку скорость увеличения массы в объеме должна обусловливаться исключительно притоком ее через поверхность, то это обстоятельство можно записать как закон сохранения в виде уравнения неразрывности:

. (4.1)

Это уравнение неразрывности можно понимать так: скорость увеличения массы жидкости в контрольном объеме обусловлена тем, что массовый расход жидкости, вытекающей из объема, меньше расхода жидкости, втекающей в него. Объемный интеграл, стоящий в левой части уравнения (4.1) и называемый нестационарным членом, обязан своим происхождением тому обстоятельству, что если течение нестационарное, то плотность жидкости в каждой точке контрольного объема V со временем изменяется. Поверхностный интеграл в правой части уравнения называется конвективным членом и выражает то обстоятельство, что поток вносит в объем V или выносит из него некоторую массу.

Если переписать уравнение (4.1) в таком виде

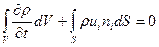, (4.2)

то можно сказать, что уравнение (4.2) демонстрирует закон сохранения массы для контрольного объема, сквозь который протекает жидкость: полная скорость изменения массы в контрольном объеме равна нулю; она состоит из двух составляющих – локальной 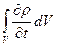, вызванной изменением плотности жидкости во всех точках объема во времени, и конвективной , обусловленной разностью массовых расходов жидкости, выносимой из объема и вносимой в него.

Используем теорему Остроградского – Гаусса для преобразования поверхностного интеграла в объемный. Вектор b_i, фигурирующий в формуле Остроградского – Гаусса, заменяется здесь на ru_i, и результат получается таким:

.

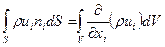Вводя это выражение в уравнение (4.2), получим уравнение неразрывности в следующей форме: .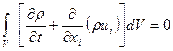

Так как это уравнение должно быть справедливо для любого объема V, то интеграл может обращаться в нуль, в соответствии с основной леммой механики сплошной среды, лишь при том условии, что во всех точках объема обращается в нуль подынтегральное выражение. Таким путем получается уравнение неразрывности в дифференциальной форме

. (4.3)

Распишем операцию дивергенции: .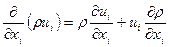

Тогда дифференциальная форма уравнения неразрывности станет такой:

, (4.3 а)

в которой полная производная 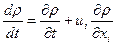является производной плотности по направлению движения, субстанциональной производной. Она говорит о том, что плотность жидкости в общем случае меняется во времени в каждой точке пространства (это локальная составляющая скорости изменения плотности 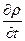) и из-за переноса ее вдоль линии тока из одной точки пространства в другую (это конвективная скорость изменения плотности )

В случае стационарного течения производные по времени равны нулю и уравнение неразрывности в интегральной форме приобретает вид

, (4.4)

а в дифференциальной форме

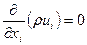. (4.5)

Если жидкость несжимаема, то уравнение неразрывности принимает простую форму:

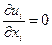. (4.5а)

Как уже отмечалось ранее, жидкость, втекающая в объем V и вытекающая из него, переносит не только массу, но и другие величины, характеризующие жидкость, как, например, количество движения, энергию и т.д. Если такую величину, отнесенную к единице объема, обозначить через g, то скорость изменения этой величины в объеме V, всегда будет выражаться в виде нестационарного объемного члена

(4.6)

и конвективного поверхностного члена

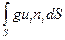. (4.7)

Величина dQ=u_in_idS представляет собой объем жидкости, переносимый в единицу времени через элементарную площадку dS; она имеет размерность м³/с и называется объемным расходом. Если угол между вектором скорости u_i и внешней нормалью n_i острый (косинус угла между ними положительный), то объем жидкости выносится через площадку dS, если же угол между вектором скорости u_i и внешней нормалью n_i тупой (косинус угла между ними отрицателен), то объем жидкости вносится через площадку dS. Поскольку g – есть характеристика жидкости, приходящаяся на единицу объема, то интеграл (4.7) будет представлять собой расход величины g, переносимой через поверхность S. Характеристика g может представлять собой любую, поддающуюся переносу, скалярную, векторную или тензорную, величину.

Поверхностный интеграл, выраженный в общей форме (4.7), может быть подобным образом преобразован в объемный при использовании теоремы Остроградского – Гаусса.

Дата добавления: 2014-01-11