Течение вязкой несжимаемой жидкости в трубах

ЛЕКЦИЯ 12

Применим уравнение движение в полных импульсах к решению следующей задачи. Вязкая несжимаемая жидкость движется по трубе постоянного сечения; тепло – и массообмен с окружающей средой отсутствует. Определить изменение давления и силу, действующую на стенки трубы в направлении оси. Течение жидкости полагаем стационарным.

Решение. Для отрезка трубы длиной l (рис.5.6) записываем уравнение движения в полных импульсах:

Рис.5.6

F2-F1=-T. Сила давления, действующая со стороны боковой поверхности на жидкость в контрольном объеме в проекции на ось трубы равна нулю. Распишем полные импульсы через составляющие: .

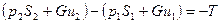По условию задачи массовый расход и площадь поперечного сечения канала по длине не изменяются. Следовательно, уравнение движения примет вид: 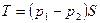, говорящий о том, что вдоль трубы давление из-за трения умень-шается, и что сила трения может быть вычислена как произведение разности дав-лений на рассматриваемом участке трубы на площадь ее поперечного сечения. Теперь определим величину разности давлений, появляющейся из-за трения.

В гидравлике принято вычислять потери энергии при течении вязкой жидкости в трубах по формуле Дарси:

,

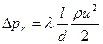в которой

Dp_r - потери энергии на работу трения, приходящиеся на 1 м ³ жидкости, Па;

l - коэффициент путевых потерь, зависящий от свойств жидкости, скорости течения и состояния омываемой поверхности;

l – длина рассматриваемого участка трубы;

D – гидравлический диаметр трубы, вычисляемый по формуле ;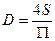

S – площадь поперечного сечения потока в трубе;

P - смоченный периметр трубы.

В единицу времени через трубу проходит объем, равный 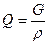м³/с. Следовательно, работа сил трения, совершаемая в единицу времени, может быть вычислена с одной стороны как 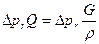, а с другой стороны, как 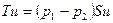. Приравнивая эти два выражения, найдем искомую разность давлений на концах трубопровода: 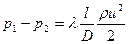. Зная значения коэффи-циента путевых потерь, и геометрические характеристики трубопровода, можно вычислить разность давлений, которую нужно создать для обеспечения заданного объемного расхода Q. Значение коэффициента путевых потерь являются в общем случае функцией числа Re и относительной шероховатости омываемой поверхности. Значение числа Рейнольдса вычисляется по формуле

.

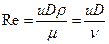В формуле u – скорость жидкости, D – гидравлический диаметр трубы, m - динамический коэффициент вязкости, n=m/r - кинематический коэффициент вязкости. Обозначив среднюю высоту бугорков шероховатости омываемой поверхности через D, а относительную шероховатость ` D = D /D, можно записать, что l=l(Re,` D ). При ламинарном режиме течения (Re £ 2300) коэффициент путевых потерь не зависит от шероховатости стенки и вычисляется по формуле Пуазейля:

.

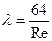При турбулентном течении, в случае, когда бугорки шероховатости не выступают за пределы пристеночной ламинарной пленки жидкости, коэффициент путевых потерь также не зависит от состояния поверхности и может быть вычислен по формуле Блазиуса:

,

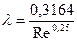при числах 4000 <Re< 10⁵ и по формуле Конакова П.К. 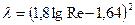, при Re> 4000. Трубы, в которых коэффициент путевых потерь не зависит от шероховатости стенок, называются гидравлически гладкими. При числах Re >10⁵ значение коэффициента путевых потерь зависит и от числа Рейнольдса и от относительной шероховатости, уменьшаясь с увеличением числа Рейнольдса, асимптотически стремясь к критическому значению. При течении с числами Рейнольдса, большими критических, коэффициент потерь уже зависит только от относительной шероховатости стенки. Критическое число Рейнольдса тем больше, чем больше относительная шероховатость. Режимы течения с числами Рейнольдса, большими критических, называются автомодельными, т.е. независимыми от числа Рейнольдса.

Дата добавления: 2014-01-11