Течение вязкого газа в трубах

Теперь рассмотрим течение сжимаемой вязкой жидкости в канале постоянного сечения без тепло – и массообмена с окружающей средой (рис.5.6).

Рис.5.6

Для участка конечной длины x уравнение движения в полных импульсах в дифференци-альной форме примет вид dF=-dT, (5.40) где dT – сила трения на участке длиной dx. В единицу времени эта сила совершает работу

.

Здесь z - коэффициент путевых потерь, а 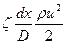- работа силы трения, приходящаяся на 1 м³ газа, Q – объемный расход газа. Из этого уравнения находим силу трения

.

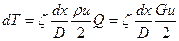Подставляя это выражение в (5.40), получим

.

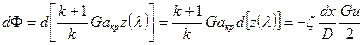Отсюда получаем

. (5.41)

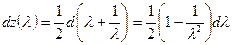Но и 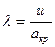. Поэтому после разделения переменных уравнение (5.41) становится таким:

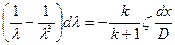. (5.42)

При турбулентном течении газа по трубам коэффициент путевых потерь можно полагать постоянным по длине трубы. Тогда уравнение (5.42) легко интегрируется, приобретая такую форму:

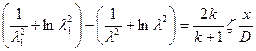. (5.43)

Введем обозначения:

и - приведенную длину.

В этих обозначениях уравнение движения (5.43) принимает простой и удобный для анализа вид:

. (5.44)

Для анализа уравнения (5.42) необходимо проанализировать вначале поведение газодинамической функции . Найдем характерные значения этой функции: при l =0, j (0) =¥; при l= 1, j (1)=1; при l=l_m, . Видим, что на границах интервала изменения аргумента функция j(l) > 0, положительна и больше 1. Поэтому экстремальное значение этой функции – при l= 1 – минимум. В дозвуковой области течения 0£ l£ 1 производная , т.е. значения j(l) уменьшаются с увеличением l; в сверхзвуковой области течения 1£ l £ l_m значения j(l) увеличиваются с увеличением l, так как в этой области производная 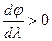.Теперь можно проводить анализ уравнения (5.44).

Целью анализа является установление зависимости изменения скорости по длине при течении газа с трением. Об изменении скорости по длине мы будем судить по изменению газодинамической функции j(l), изменение которой вдоль трубы задается уравнением (5.44). По этому уравнению видно, что вдоль трубопровода, при удалении от начального сечения 1, значение j(l) уменьшается, стремясь, как показал анализ поведения j(l), к минимальному своему значению, равному 1. Поэтому, если поток на входе в трубопровод дозвуковой, то к выходу из трубопровода он ускоряется, и достигает максимальной скорости на срезе трубы. Значение максимальной скорости определяется минимально возможным значением функции j(l), равным 1. Следовательно, максимальная скорость дозвукового потока на выходе из трубы равна скорости звука, т.е. критической.

Режим течения в трубе, когда на выходе из нее скорость газа равна скорости звука (критической), называется критическим, а длина трубы на этом режиме – критической длиной. Для заданной скорости на входе в трубу l ₁ значение приведенной длины на критическом режиме, критической длины, определится из уравнения (5.44), в котором нужно положить j(l) = 1:

c_кр = j(l ₁ ) -1,

.

При заданной длине трубы значение приведенной скорости на входе при критическом режиме также находим из уравнения (5.44):

.

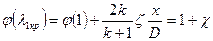Очевидно, что если на входе в трубу поток сверхзвуковой, то в соответствии с уравнением движения (5.44), скорость его должна уменьшаться, и на выходе из трубы не должна быть меньше скорости звука.

При течении вязкого газа в трубах можно выделить следующие типы течений (рис.5.8).

Рис.5.8

I. Дозвуковое докритическое течение. Дозвуковой поток ускоряется к выходу, но не достигает скорости звука. II. Дозвуковое критическое течение. Дозвуковой на входе в трубу поток достигает на срезе скорости звука. III. Дозвуковой на входе поток имеет скорость, большую скорости при критическом течении. Этот тип течения невозможен, поскольку не отвечает уравнению движе-

ния (5.42). При фиксированной приведенной длине c когда l₁>l_1кр значение газодинамической функции j ( l ) на выходе будет меньше единицы, что не соответствует области ее определения, приводит к нарушению закона количества движения (5.42). Явления, не подчиняющиеся уравнениям законов сохранения, существовать не могут.

IV. Сверхзвуковое докритическое течение. Сверхзвуковой на входе поток замедляется к выходу, но не достигает скорости звука на выходе, остается сверхзвуковым.

V. Сверхзвуковое критическое течение. Сверхзвуковой поток в трубе замедляется до критической скорости на срезе.

VI. Сверхзвуковое субкритическое течение. Сверхзвуковой на входе поток имеет скорость, меньшую скорости на входе при сверхзвуковом критическом течении. В таком течении поток тормозится внутри трубы до какого-то l> 1, а затем скачком уменьшает свою скорость до l^¢< 1 такой, что l×l¢= 1. Дальнейшее движение газа к выходу описывается кривой, отвечающей течению II.

Дата добавления: 2014-01-11