Анализ точности. Кривые распределения. Точностные диаграммы

Определение суммарной погрешности механической обработки

Суммарная погрешность подсчитывается с учетом имеющих место первичных погрешностей при выбранных способе и схеме обработки и определяет правильное их выбора путем сравнения с заданным полем допуска на данном переходе. Эту задачу можно решать аналогично расчету замыкающего звена размерной цепи, составляющими звеньями которой являются величины первичных погрешностей.

Определим суммарную погрешность обработки заготовок при условии их обработки в приспособлении на настроенном станке за большое число настроек. В нее войдут:

Δ_l - погрешность из-за упругих отжатий в технологической системе, зависящая от изменения силы резания вследствие неодинакового неравномерною припуска, неодинаковой твердости заготовок, притупления инструмента. Она приводит к изменению размера и формы заготовки. Распределение размеров детали и величин отклонений формы под влиянием этой погрешности подчиняется нормальному закону распределения случайных величин;

ε_υ, - погрешность установки, складывающаяся из случайных величин и представляющая величину случайную, подчиняющуюся закону нормального распределения.

Δ_н - погрешность настройки, при большом числе настроек является величиной случайной, подчиняющейся закону нормального распределения. Если обработка партии заготовок ведется за одну настройку, то Δ_н - величина постоянная, равная фактической погрешности установки инструмента на размер;

Δ_и - погрешность из-за износа режущего инструмента (в период установившегося нормального износа) подчиняется закону равной вероятности, а распределение деталей по размерам вследствие ее влияния имеет вид прямоугольника,

Δ_т - погрешность из-за температурных деформаций звеньев технологической системы. После достижения теплового равновесия- величина постоянная, при перерывах в работе и до достижения теплового равновесия - изменения размеров деталей идет по кривым, аналогичным изображенным на рисунке 2.13,в,г. Их закономерности мало изучены и недостаточно определенны.

Σ_ΔФ - сумма погрешностей формы, вызываемых геометрическими неточностями станка, деформациями заготовки при закреплении, неравномерными отжатиями упругой системы. При работе на одном станке может быть взята как величина систематическая постоянная. При ее определении следует учитывать взаимную компенсацию отдельных составляющих.

Тогда суммарную погрешность обработки можно определить по

следующей формуле

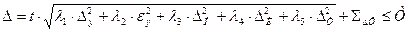
где t - коэффициент, определяющий процент риска получения брака. При t = 1 процент риска равен 32, при t = 2 он равен 4,5, при t = 3 он равен 0,27. Примем t = 3;

λ - коэффициенты, зависящие от законов распределения погрешностей. При нормальном λ = 1/9; при равной вероятности и неизвестном λ = 1/3. Таким образом, λ₁ = λ₂ = λ₃ = 1/9; λ ₄ = λ ₅ = 1/3; Т - допуск на выполняемом переходе.

Подставив значения коэффициентов, получим

,

Однако во многих случаях имеют место не все первичные погрешности обработки. Так, при обработке диаметральных размеров исключается ε_у. При обработке партии заготовок с одной настройки учитывается не Δ_н, а только погрешность установки инструмента на размер. При сверлении, зенкеровании и развертывании при работе с применением охлаждения учитываются только увеличения диаметров вследствие разбивки, допуск на размер инструмента, износ инструмента.

При обработке методом пробных рабочих ходов

,

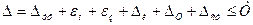где Δ_уф — погрешность формы заготовки из-за копирования первичных погрешностей формы, полученных на предшествующем переходе и операции;

ε_п - погрешность установки инструмента на размер;

ε_s - погрешность формы из-за деформации заготовки при ее зажиме;

Δ_и - погрешность формы из-за износа режущего инструмента;

Δ_т - погрешность из-за тепловых деформаций системы при обработке одной заготовки;

Δ_ст - погрешность формы из-за геометрической неточности станка.

Погрешности суммируются алгебраически с учетом их частичной или полной компенсации.

Доли первичных погрешностей в суммарной непостоянны и зависят от ряда технологических факторов. От суммарной погрешности они составляют в % Δ_и – 10-20; Δ_и – 30-40 при чистовой и 20-30 при предварительной обработке; Δ_т – 10-15; ε_у – 20-30; при обработке нежестких и тонкостенных заготовок погрешность из-за остаточных напряжений достигает 40; погрешности из-за геометрических неточностей станков – 10-30 %.

После определения и расчета первичных и суммарных погрешностей необходимо оценить долю, вносимую отдельными погрешностями в суммарную и выявить доминирующие составляющие. Затем осуществляют необходимые мероприятия по их уменьшению и при необходимости корректируют технологический процесс с целью достижения заданной точности на проектируемой операции.

Анализ точности методами математической статистики

Для принятия окончательных решений с точки зрения обеспечения необходимой точности на операции по принятой схеме обработке изложенный выше расчетный метод определения суммарной погрешности не всегда дает исчерпывающие результаты:

• трудно учесть и рассчитать все факторы, влияющие на точность обработки, вследствие того, что многие из них носят случайный характер,

• расчеты довольно трудоемки и требуют измерения некоторых фактических данных, например, таких, как геометрические неточности станка;

• фактические погрешности часто не совпадают с расчетами и требуют проверки.

Все это вызывает необходимость дополнительного проведения статистического исследования точности обработки.

Основными задачами такого исследования являются

• определение устойчивости и стабильности технологической операции и выявление причин, нарушающих стабильность;

• определение поля рассеивания погрешностей и сравнение его с величиной поля допуска,

• определение необходимости внесения изменений в настройку станка.

Погрешности при обработке можно разделить на три вида: систематические постоянные (из-за неточности приспособления, станка, инструмента), систематические закономерно изменяющиеся (из-за износа инструмента, из-за температурных деформаций системы) и случайные (из-за упругих деформаций системы, установки, настройки при большом количестве настроек). Систематические постоянные погрешности могут быть выявлены измерением деталей после обработки, и их влияние может быть уменьшено технологическими мерами Выявление законов изменения систематических закономерно изменяющихся погрешностей также позволяет принять меры к их устранению или уменьшению. Определить случайную погрешность для каждой отдельной детали в партии нельзя. Однако аналитическим путем и с учетом опытных данных можно с определенной вероятностью определить границы колебаний этих погрешностей.

Кривые распределения и оценка точности на их основе

Статистический метод оценки точности применяется в условиях производства большого количества деталей. Для его применения необходимо произвести выборку деталей из обрабатываемых на исследуемой операции. Количество деталей в выборке влияет на точность оценки и определяется по специальной методике. По результатам измерения деталей выборки строится опытная кривая распределения, к которой по критерию согласия подбирается теоретический закон распределения.

Опытные кривые распределения строят следующим образом.

По оси абсцисс откладывают измеряемую величину, например диаметр деталей, через определенные интервалы, а на оси ординат их количество, попадающее в эти интервалы, или частости.

Частость - это отношение числа деталей одного размера к общему числу деталей выборки. Соединяя точки пересечения, получают ломаную линию, которая называется опытной кривой распределения или полигоном распределения деталей по размерам (рисунок 7.1, а). Определяют поле рассеяния размеров деталей как приближенную меру их точности.

При обработке деталей в машиностроении их размеры распределяются наиболее часто по нормальному закону Гаусса, Кривая распределения представлена на рисунке 6.1,б. Этому же закону подчиняются распределения массы заготовок, твердости и других механических свойств, высоты микронеровностей, погрешности измерений и некоторых других величин. Уравнение кривой Гаусса

,

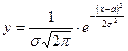где е - основание натуральных логарифмов;

а - значение абсциссы, при которой у = мах;

σ - среднее квадратичное отклонение исследуемой величины;

,

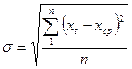где n - число измерении;

х_t - значение текущего измерения;

х_ср - среднее арифметическое из произведенных измерений;

,

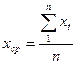При n=50 погрешность определения σ равна 10%,при n=25 она равна 15%. При малом числе измерений n<10 вычисление σ дает большую ошибку.

При х=а, 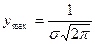. Точки перегиба кривой лежат на расстояниях σ от оси симметрии, их ординаты

.

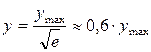Среднее квадратичное отклонение σ является мерой точности обработки. На рисунке 3.1,в показаны кривые распределения σ, σ₁, σ_2, σ₃.

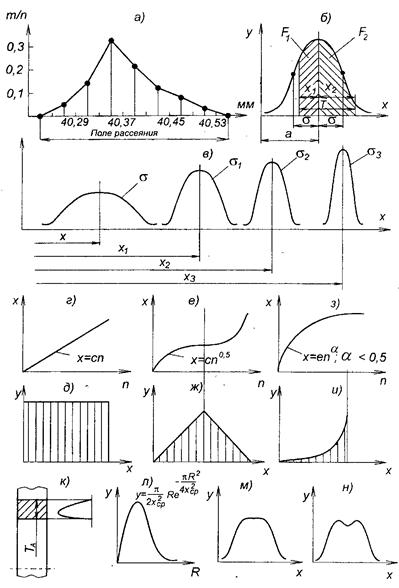
Рисунок 7.1 - Кривые распределения и их разновидности

Дата добавления: 2014-01-11