Применение теории размерностей в бурении

Рассмотрим применение положений теории размерностей на примере силы удара падающего инструмента о породу забоя (разрушением породы будем пренебрегать):

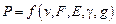, (35)

где v - скорость падения инструмента; F - площадь поперечного сечения инструмента; E - модуль упругости материала инструмента; γ- удельный вес материала инструмента; g - ускорение свободного падения.

Функциональную зависимость (35) представим в виде степенного одночлена

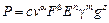, (36)

где с - безразмерный коэффициент пропорциональности, определяемый опытным путем; α, β, n, m, z - показатели степеней.

В уравнение (36) входят 5 размерных величин. Искомые величины имеют следующие размерности:

(37)

Подставим размерности в уравнение (36):

. (38)

Для показателей массы

1 = n + m. (39)

Для показателей линейного размера

1 =. (40)

Для показателей времени

–2 =. (41)

Из (39) следует, что

n = 1 – m. (42)

Из (39) и (41)

,

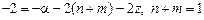тогда 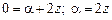. (43)

Из совместного решения (40), (42) и (43) получаем

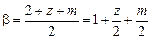. (44)

Уравнения (42)-(44) дают возможность выразить показатели α, β и n через два остальных показателя m и z. Используя зависимости (42)-(44) представим уравнение (36) в виде

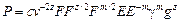. (45)

Сгруппируем сомножители уравнения (45) в комплексы, имеющие своей степенью либо только z, либо только m. Полученные таким образом комплексы не имеют размерности и, следовательно, являются критериями подобия:

. (46)

Таким образом, получены 3 критерия подобия и в критериальной форме уравнение (46) может быть записано как

, (47)

где П ₁, П ₂, П ₃ - критерии подобия.

Можно отметить, что значения показателей n и m, а также коэффициента с остались неизвестными. Их можно определить экспериментальным путем.

Дата добавления: 2014-01-11