Пересечение поверхности плоскостью

Лекция № 8. ПЕРЕСЕЧЕНИЕ ПОВЕРХНОСТИ ПЛОСКОСТЬЮ. РАЗВЕРТЫВАНИЕ ПОВЕРХНОСТЕЙ. СПОСОБЫ ПОСТРОЕНИЯ РАЗВЕРТОК

План лекции

1. Пересечение поверхности плоскостью.

1.1. Способ ребер.

1.2. Способ граней.

2. Способ вспомогательных секущих плоскостей.

3. Развертывание поверхностей. Способы построения разверток.

3.1. Способ треугольников.

3.2. Способ нормального сечения.

3.3. Способ раскатки.

В общем случае, при пересечении поверхности плоскостью, определяют ряд общих точек, Î поверхности и плоскости. Полученные точки соединяют ломаной линией, если поверхность гранная, и под лекало, если поверхность криволинейная. В результате получается фигура, которая называется сечением. Для построения точек, Î линии сечения, используют следующие способы:

1. Способ ребер.

2. Способ граней.

3. Способ вспомогательных секущих плоскостей.

Рассмотрим случаи, когда секущая плоскость занимает частное положение.

Пример. Построить проекции линии пересечения поверхности пирамиды плоскостью.

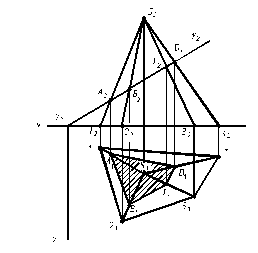
Рис. 8.1

Плоскость a ^ П₂ и обладает собирательным свойством, следовательно фронтальная проекция сечения совпадает со следом плоскости – это проекция A₂ B₂ C₂ D₂. Вторая проекция сечения A₁ B₁ C₁ D₁ строится при помощи линий проекционной связи.

Конические сечения:

1. Окружность – секущая плоскость параллельна плоскости основания.

2. Эллипс - секущая плоскость наклонена к плоскости основания.

3. Две прямые – секущая плоскость проходит через вершину и основание конуса.

4. Двойная прямая - секущая плоскость касается образующей.

5. Точка - секущая плоскость проходит через вершину конуса.

6. Парабола - секущая плоскость параллельна образующей конуса.

7. Гипербола - секущая плоскость параллельна оси вращения.

Пример. Построить проекции линии пересечения конуса плоскостью.

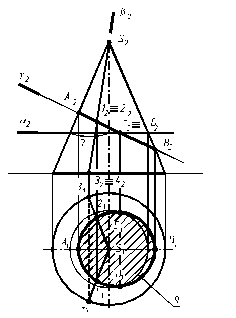
Рис. 8.2

Построение начинаем с опорных точек: очерковые, высшая, низшая и т. д. Фронтальная проекция эллипса совпадает с фронтальным следом плоскости. Горизонтальную проекцию можно построить по большой и малой оси или при помощи промежуточных точек.

АВ - большая ось эллипса, точки А и ВÎ очерковым образующим. С и D Î малой оси эллипса, точки 1, 2 Î промежуточным образующим.

Пример. Построить проекции линии пересечения цилиндра плоскостью.

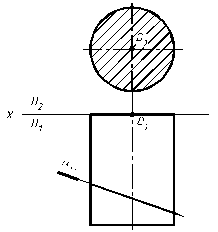
Рис. 8.3

В данном случае плоскость a ^ П₁. Следовательно горизонтальная проекция линии сечения совпадает с горизонтальным следом плоскости. Кроме того, так как цилиндр занимает проецирующее положение, то фронтальная проекция линии сечения совпадает с очерком цилиндра на фронтальной плоскости проекций.

Рассмотрим случай, когда плоскость занимает общее положение.

Дата добавления: 2014-01-11