Метод Данилевського

За цим методом матриця А подібними перетвореннями 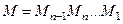приводиться до вигляду у формі Фробеніуса 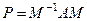, причому :

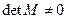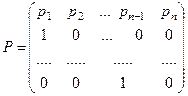(3)

У матриці (3) елементи під головною діагоналлю - одиниці. Характеристичний поліном для (3) будується розкриттям характеристичного визначника матриці Р по першому рядку. Він, внаслідок подібності матриць А та Р, є також і характеристичним поліномом матриці А.

Приведення до вигляду (3) здійснюється послідовним перетворенням рядків, починаючи з останнього. На першому кроці множимо матрицю А справа на матрицю

,

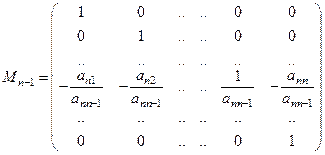При цьому останній рідок матриці 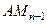матиме вигляд

.

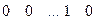Для збереження подібності множимо 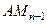зліва на матрицю

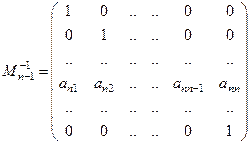
Останній рідок при цьому не змінюється. Аналогічно потрібно перетворити і інші рядки матриці А.

Примітка

В методі може виникати ділення на нуль.

Ітераційний метод Якобі.

Діє для симетричних матриць.

Обертанням будемо називати перетворення координат за допомогою матриці

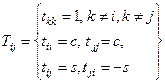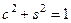, . (4)

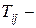матриця обертання.

Метод заснований на підборі нескінченної послідовності обертань, які перетворюють вихідну матрицію на діагональну. На діагоналі цієї матриці містяться відповідні власні числа матриці.

Сферичною нормою матриці А будемо називати величину

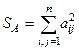. (5)

Розіб’ємо (5) на діагональну та недіагональну частини:

, .

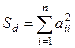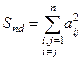Ітераційний метод Якобі передбачає збереження сферичної норми при обертаннях при зменшенні недіагональної частини.

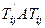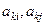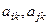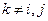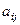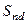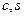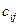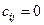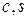При елементарному перетворенні С=недіагональні елементи та при змінюються так, що попарні суми їхніх квадратів зберігаються. Окрім цих елементів ззовні діагоналі змінюється ще . Щоб максимально зменшити за одне обертання, підберемо елементи обертання (4) таким чином, щоб анулювати елемент (). Оскільки , то для визначення маємо систему:

,

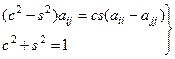звідки

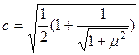, де 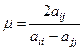, 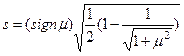. На кожному обертанні потрібно перетворювати на нуль максимальний за модулем недіагональний елемент, або, що є більш ефективним з обчислювальної точки зору, обирати найбільшу із сум квадратів недіагональних елементів за кожним рядком 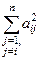, та у відповідному рядку визначати найбільший за модулем елемент-оптимальний.

Збіжність методу. Оптимальний елемент 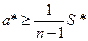(суми свого рядка), а ця сума 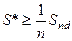. Тобто за одне обертання недіагональна частина сферичної норми спадає не менш ніж на 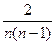. Після 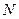обертань величина 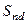становитиме

; .

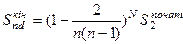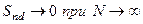Примітка. Пошук власних векторів

Оскільки вектори 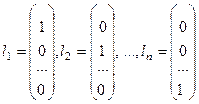- власні вектори діагональної матриці, то власні вектори матриці А- стовпці матриці обертань 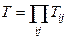. Легко одержати, що .

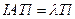Прямий метод Якобі (обертань)

Метод широко використовується для побудови характеристичного многочленну симетричної матриці А. Вихідна матриця за допомогою обертань приводиться до три діагонального виду. Подібність матриць при цьому зберігається.

Нехай 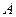- симетрична матриця. Розглянемо 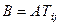. . 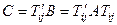Оскільки 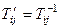, то 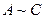(подібні). Стовпці матриці А співпадають зі стовпцями В за виключенням i та j стовпця:

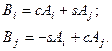
Рядки матриць С та В співпадають за виключенням 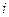та 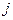рядка:

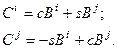
Нехай 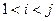. Покажемо, що можна добрати так, щоб 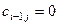. Дійсно, 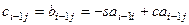. З умови 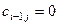одержимо

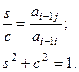
Тому

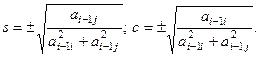Вибір знаку не має значення.

Процес тридіагоналізації можна провести наступним чином: за допомогою перетворень 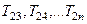анулюють по черзі елементи першого рядка, починаючи з третього. Потім за допомогою 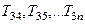анулюються елементи другого рядка, починаючи з четвертого і так далі. Ми перейдемо від даної симетричної матриці до тридіагональної:

, .

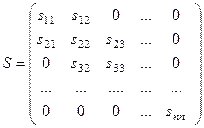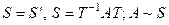Для характеристичного многочлена 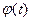три діагональної матриці 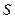побудуємо рекурентну формулу. Записуючи формально 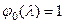та розглядаючи матриці розмірностей 1,2,3, …, знаходимо:

;

;

.

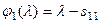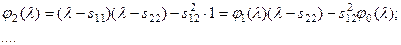
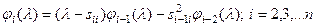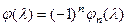Послідовність 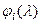- послідовність поліномів Штурма для характеристичного полінома.

Дата добавления: 2014-01-11