QR-алгоритм

Це один із найкращих методів визначення власниз чисел. Ідея цього алгоритму - привести вихідну матрицю А до клітинково-трикутного вигляду В із діагональними блоками 1х1 або 2х2. Причому ця матриця подібна до даної. Власні числа - або діагональні елементи В (у випадку блоків 1х1), або корені квадратних рівнянь.

Етапи алгоритму:

1. Перетворення ортогональними обертаннями до форми Гессенберга H(верхня трикутна матриця з субдіагоналлю): . Позначимо проміжну матрицю, яка утворюється з А в процесі переходу до форми H: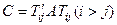. Щоб її елемент 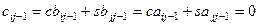, треба одержати з рівнянь:

Покладаючи 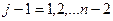, 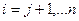обертаємо в нуль послідовно елементи першого стовпця, починаючи з третього, далі елементи другого стовпця, починаючи з четвертого і т.д. Порядок занулення має значення і є наступним:

1)(3,1), (4,1), …, (n,1);

2) (4,2), (5,2), …, (n,2);

……………………….

n-2) (n,n-2).

2.QR-факторизація. Будь-яку дійсну матрицю можна представити у вигляді добутку 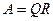, де 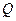- ортогональна матриця, 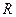-верхньотрикутна.

Перепишемо . Задача тепер переформулюється так: визначити 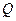так, щоб була верхньотрикутною. Аналогічно до етапу 1 скористаємось перетвореннями обертання,

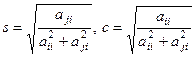, , що забезпечує 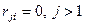матриці R.

Порядок занулення:

1)(2,1), (3,1),…, (n,1);

2)(3,2), (4,2), … (n,2)

……………………..

3)(n,n-1).

Таким чином, 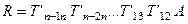, тобто .

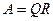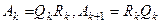Після розкладення будують матрицю , . Продовжуючи процес, одержують послідовність матриць , . Послідовність матриць 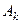прямує до матриці клітинково-трикутної форми.

Метод інтерполяції

Використовується для побудови характеристичного многочлена матриць невеликої розмірності (n<10). Зручний для випадку, коли 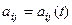. Для матриці порядку характеристичний многочлен має ступінь , а кожен многочлен -го ступеня однозначно визначається своїми коефіцієнтами . Неважко бачити, що значення характеристичного полінома в деякій точці можуть бути знайдені лише за матрицею А:

.

Нехай 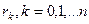- довільні числа з відрізку, що містить власні числа матриці А (в якості такого відрізку можна взяти ), причому доцільно розташовувати на обраному відрізку приблизно рівномірно. Обчислимо значення:

.

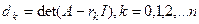Визначники 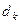слід обчислювати методом виключень Гауса. Після цього характеристичний многочлен виписують за допомогою інтерполяційної формули, наприклад поліному Лагранжа:

.

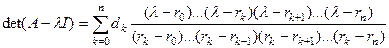Многочлен в правій частині при 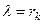приймає значення 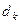, тобто є шуканим.

З формули для похибки інтерполяційного многочлену

витікає, що R=0 (похідна (n+1) порядку від многочленна n ступеня), тобто характеристичний многочлен відновлюється за методом інтерполяції точно.

Недолік метода – великий обсяг обчислень.

Метод зворотніх ітерацій

Застосовується для значходження власних векторів.

Оберемо довільний вектор 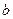і розглянемо лінійну систему:

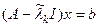, де 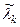- наближене значення власного числа, . Система має єдиний розв’язок. Покажемо, що знайдений з цієї системи вектор 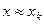- власному вектору, який відповідає власному значенню .

Обмежимось випадком, коли матриця n-го порядку має n лінійно-незалежних власних векторів 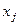. Тоді власні вектори утворюють базис за яким можна розкласти вектори та :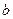

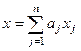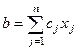, . Підставивши ці розяладення в вихідну систему та враховуючи 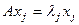, одержимо:

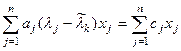. Звідси внаслідок лінійної незалежності 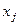слідує, що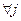

. З цієї формули видно, що при 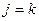і коефіцієнт -великий. Інакше він є малим. При зворотній ітерації, тобто при переході від 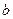до компонента 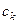різко збільшується порівняно з іншими компонентами, і вектор виявляється близьким до 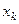. Якщо вектор 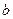обрано невдало, знайдений може відрізнятися від 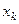. Тоді ітерації слід повторити за формулою:

.

Зазвичай 2-3 ітерацій буває достатньо. Знайдені вектори обов’язково нормують, щоб не виникало дуже великих чисел, які можуть призвести до переповнення розрядної сітки.

Метод лінеаризації

Запишемо задачу знаходження власних значень

у координатній формі:

,

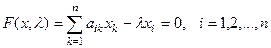де 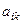- елементи матриці А, - координати . Задача зводиться до розв’язання системи рівнянь з невідомими 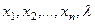. Ця система нелінійна (є члени виду ). Застосуємо метод Ньютона розв’язання нелінійних систем.

Нехай - малі прирости змінних , -приріст . Тоді система набуває виду:

-номер ітерації - система відносно прирощень 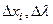. Початкове наближення 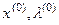- задається. Система містить n рівнянь та n+1 невідомих, але, оскільки власний вектор визначається з точністю до множника, то не порушуючи загальності, можна покласти 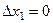. Нові наближення для одержуються як

,

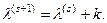
Процес повторюється до спів падання двох послідовних ітерацій із заданою точністю.

Дата добавления: 2014-01-11