Алгоритмичные и программные методы построения динамических сцен в реальном времени

Рассмотрим задачу поворота символа с шагом 22,5⁰, описанного матрицей 16´16 точек.

Первая матрица изображения символа (16´16 или 20₈´20₈) в восьмеричной системе счисления имеет вид:

А _0,0; A _0,1; ……; A _0,16; A _0,17

А _1,0; A _1,1; ……; A _1,16; A _1,17

…………………….……

А _16,0; A _16,1; …..; A _16,16; A _16,17

А _17,0; A _17,1; ……; A _17,16; A _17,17,

а в условных (т.е. не привязанных к конкретной точке экрана) восьмеричных адресах эта матрица выглядит так:

0, 1, ……16, 17

20, 21, …… 36, 37

………….………….

340, 341, …... 356, 357

360, 361, …... 376, 377.

Аналогично представлены следующие - вторая и третья матрицы изображения. Как было показано выше из базовых символов, повернутых на углы 0⁰ и 45⁰ и имеющих две оси симметрии, получаются по 4 изображения символа с азимутальными направлениями 0⁰, 90⁰, 180⁰, 270⁰ и 45⁰, 135⁰, 225⁰, 315⁰ соответственно. А из изображения базового символа, повернутого на угол 22,5⁰ и имеющего три оси симметрии, получается 8 символов с азимутальными направлениями 22,5⁰; 67,5⁰; 112,5⁰; 157,5⁰; 202,5⁰; 247,5⁰; 292,5⁰; 337,5⁰.

При необходимости отобразить поворот по определенному признаку (конкретной величине угла поворота или номеру его азимутального направления) выбирается базовая матрица символа и соответствующий порядок ее считывания. Затем с помощью подпрограммы типа «цикл в цикле» считывается записанная в ОЗУ базовая матрица и на экране дисплея отображается изображение выбранного символа в нужном азимутальном направлении. Предлагаемый метод реализован в программе, по которой из трех базовых матриц изображений символа на экране видеотерминала формируется 16 изображений такого символа, ориентированных в различных азимутальных направлениях. Программа отображает последовательную выдачу всех 16 изображений, в целом отображающую маневр объекта в реальном времени.

Исследования показали, что скорость вычислений получается максимальной в том случае, когда основные составляющие программы сформированы в отдельные модули, которые представляют собой независимые фрагменты.

Известно, что движение символов на экране геоинформационного комплекса можно задать с помощью последовательности операций поворота и параллельного переноса. Операция параллельного переноса является простой для программной реализации и достаточно быстрой, поскольку требует не более двух операций сложения целых чисел для каждой точки символа. Операция поворота символа требует большого количества машинных ресурсов, поскольку требует для своего выполнения в общем случае четыре операции умножения действительных чисел.

Количество операций в алгоритме поворота существенно сократится по сравнению с известными методами, если использовать алгоритм Брезенхема для построения прямых.

Выберем точку начала относительной системы координат 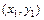. Для удобства вычислений можно взять одну из вершин прямоугольной матрицы, в которой хранится растровое изображение символа 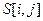. Для этой точки вычисляются ее координаты 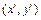после поворота с помощью синусно-косинусного преобразования.

Предлагается подсчитать значения тангенса и котангенса угла поворота 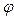и присвоить dx1:=h1∙tg( 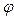); dy1:=h2∙ctg( 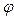). Матрица растрового изображения символа 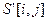, которая соответствует символу после поворота на угол 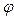вычисляются по циклу:

x1:=x’-dx2; y1:=y’-dy2;

от i:=0 до X начать

j:=0; x:=x+dx1; y1:=y1+1;

если int{x}=int{x-dx1} то x1:=x1+1;

x2:=x1;y2:=y1;

S'[i,j]:=S[x1,y1];

от j:=1 до Y начать

x2:=x2+1; y:=y+dy1;

если int{y2}=int{y2-dy1} то y2:=y2+1;

S’[x2,y2]:=S[i,j];

конец цикла;

конец цикла;

Предлагаемый алгоритм быстрого экономичного поворота обеспечивает меньшее количество операций за счет того, что в нем совершается лишь одно сложение вещественных чисел, а две другие операции сложения в теле цикла осуществляются для целых чисел, что позволяет производить их выполнение в четыре раза быстрее, (в рассматриваемом примере использовались 16-ти разрядные числа). С учетом изложенного количество операций при выполнении поворота будет равно , где 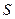- количество элементов в матрице символа, в то время как известные методы поворота предусматривают не менее 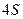операций, то есть время выполнения составит 22% от времени выполнения описанных в литературе алгоритмов.

Дата добавления: 2014-01-11