Проекции. Пусть в пространстве заданы плоскость и прямая , не параллельная этой плоскости

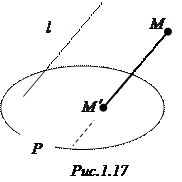Пусть в пространстве заданы плоскость 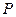и прямая 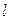, не параллельная этой плоскости. Проекцией произвольной точки 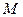на плоскость 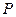параллельно прямой 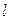называется точка 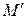пересечения плоскости 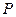и прямой, проходящей через 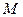параллельно 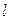(рис. 1.17).

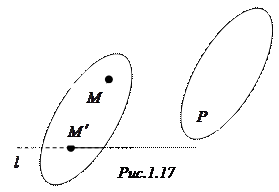
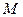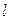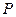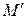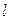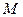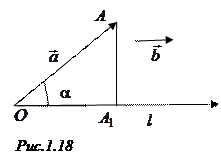
Проекцией произвольной точки на прямую параллельно плоскость называется точка пересечения прямой и плоскости, проходящей через параллельно 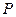(рис. 1.18). Проекцией множества точек на плоскость (или на прямую) называется множество проекций всех точек этого множества на заданную плоскость (или прямую). Если плоскость 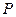и прямая 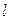перпендикулярны, то проекции называются ортогональными. В дальнейшем мы будем рассматривать только ортогональные проекции. В этом случае проекция точки 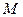на прямую совпадает с основанием перпендикуляра, проведенного из точки 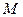к этой прямой.

Пусть в пространстве задана прямая 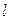. Если на ней выбрать направление с помощью вектора 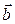(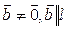), то прямая превратится в ось. Любой вектор 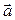, как и всякое множество, на эту ось можно спроектировать. Полученный вектор будем называть векторной проекцией вектора 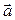на вектор 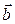и обозначать 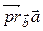. На рисунке 1.18 , .

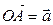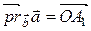Алгебраической проекцией (или просто проекцией) вектор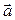ана 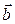называется число

.

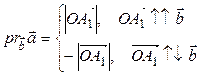Проекции векторов обладают следующими свойствами.

1. 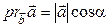, где 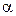– угол между векторами 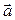и .

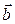► Если 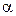острый угол, то (рис. 1.18) 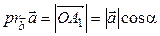; если 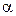– тупой, то (рис. 1.19) 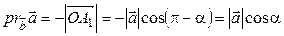. Если же 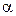- прямой угол, то .◄

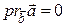2. 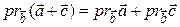, т.е. проекция суммы векторов равна сумме их проекций.

►Выберем в пространстве ортонормированный базис так, чтобы 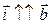. Если в этом базисе вектор 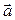имеет координаты 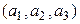, то, нетрудно убедиться, что 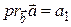(рис. 1.20).Тогда доказываемое свойство вытекает из свойств координат векторов.◄

3. 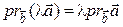, т.е. при умножении вектора на число его проекция умножается на это число.

Это свойство также вытекает из свойств координат векторов.

Дата добавления: 2014-01-13