Квантование по уровню

Квантование по уровню – преобразование непрерывного информационного множества аналогичных сигналов в дискретное.

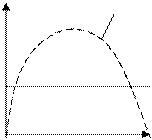
Суть при этом диапазон возможных изменений функции – интервал (а, в) – разбивается на n-интервалов квантования.

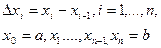
В результате квантования любое из значения х, принадлежащее интервалу () округляется до некоторой величины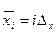

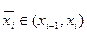
Величины 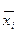- уровни квантования.

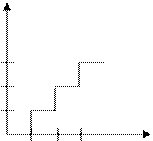
При квантовании по уровню производится отображение всевозможных значений х на дискретизации, состоящую из .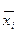

Замена истинных значений х соответствующими дискретными значениями вносит ошибку (шум) квантование

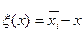
При равномерном квантовании

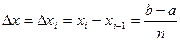
Определим ошибку квантования по критерию наибольшего отклонения

При заданной n наибольшая ошибка квантования 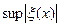минимальна, если 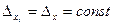уровень квантования 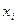, выбирается в середине интервала

Исходный сигнал

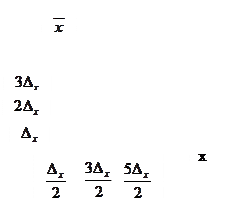
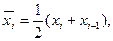тогда

Статистические характеристики шума квантования для некоторого фиксированного момента

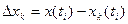
Согласно принципу квантования всякий раз, когда исходный сигнал находится в интервале от 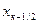до , будет передаваться одно значение уровня 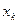к- номер квантования. При этом возникает ошибка в значении сигнала.

Математическое описание ошибки :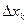

,

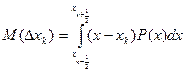среднее значение (квадратическое)

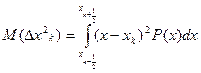, где 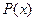- функция плотности вероятности сигнала x(t) в момент .

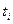Пологая интервал от 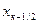до малым по сравнению с диапазоном применения x(t), можно принять 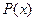на этом интервале постоянной n равной по своему значению для некоторого среднего уровня 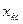. Тогда

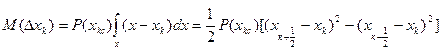(2)

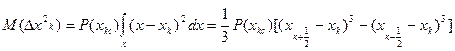(3)

где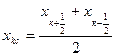

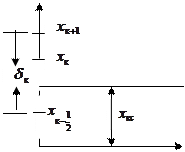
Обозначим через 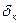шаг квантования для к уровня.

В общем случае 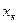может не находится середине уровня квантования.

Найти такое распределение 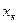, при котором дисперсия на этом уровне минимальна

Из (3) будем иметь

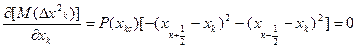
отсюда

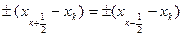
1. При одинаковых знаках справа и слева 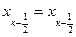(квантование отсутствует)

2. При разных знаках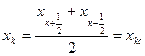

В этом случае математическое ожидание равно 0. Таким образом; минимальная дисперсия будет в случае, если уровень 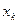расположен на середине шага квантования:

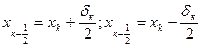и дисперсия

(4)

Суммируя (4) по всем уровням получим дисперсию шума квантования

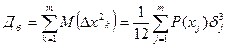(5)

При шаге 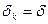(равномерный)

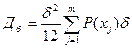
Пологая, вероятность появления значении сигнала x(t), превосходит максимальный уровень 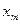, пренебрежительно малым, запишем

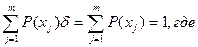
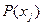- вероятность того что x(t) находится на интервале 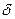, тогда для равномерного квантования

.

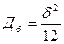Дата добавления: 2014-01-13