Стационарные случайные процессы

В ИС часто встречаются случайные процессы, протекающие во времени приблизительно однородно. Они имеют вид непрерывных случайных колебаний около некоторых средних значении, причем ни среднее значение, ни характер этих колебаний не претерпевают сущность гуманной во времени.

Такие процессы – стационарные. (Шум электрических устройств)

В любой динамической системе случайный процесс начинается с так называемого «переходного» процесса, затем переходит в установленный режим, который с некоторым приближением можно считать стационарным. Строго: стационарно случайные процессы бесконечны во времени, т.е. не имеют ни начала, ни конца таких процессов практически нет. Однако многие случайные процессы на определенных отрезках времени с определенной приближенностью можно считать стационарным.

Под стационарностью в узком смысле понимаются случайные процессы, для которых функции распределения плотности вероятности

W_n(x₁,t₁; x₂,t₂;...;x_n,t_n) произвольные порядка n не меняется при любом сдвиге всей группы точек t₁,t₂,...t_n вдоль оси t₁ т.е. для любых n и .

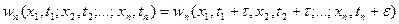
Из определения следует, что:

1. Одномерная функция распределения плотности вероятности не зависит от времени:

2. Двумерная функция распределения плотности вероятности зависит только от разности времени t₂-t₁=, т.е.

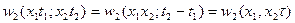
3. Трехмерная функция распределения плотности вероятности зависит только от двух разностей времен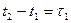и и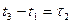

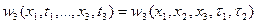
Поскольку математические ожидание и дисперсия выражаются через одномерную функцию распределения плотности вероятности то на основе (1) можно утверждать, что для стационарного СП математические ожидание и дисперсия не зависит от времени.

На основании (2), колебательные распределения функция случайного процесса зависит только от разности времен , т.с.

(*)

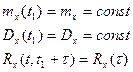На практике часто встречаются случайные процессы, для которых в выражении (*) моменты вероятности плотности зависят от времени. Поэтому понятия стационарности целесообразно расширить, приняв за основу определения стационарности условия (*)

Стационарность в широком смысле (ХИНЧИН) согласно которому стационарными процессами являются случайные процессы, у которых математические ожидание и дисперсия не зависят от времени, а корреляционная функция зависит только от разности времени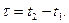

Случайные процессы стационарные в узком смысле будут стационарными в широком смысле, но не наоборот.

Стационарные процессы по своей природе проще чем нестационарные и описываются более простыми характеристиками.

Среди стационарных процессов многие удовлетворяют условию эргодичности.

Следовательно, для стационарного эргодичности процессов справедливее соответствия.

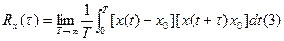
(1)-(3) лежат в основе корреляционной теории сигналов.

Дата добавления: 2014-01-13