Свойство корреляционных функции случайного процесса

I По мере увеличения зависимость между x(t) и x(t+) ослабевает при эти величины становятся незаменимыми.

Таким образом, при КРФ стремится к квадрату математического ожидания стационарного процесса (КРФ равна мощности постоянной составляющей реализации стационарного процесса)

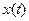II При уменьшении зависимость между и усиливается и в пределе при 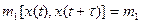[x²(t)]=m₂[x(t)]=R_x

При КРФ =0 начало моменту второго порядка функции х(t). Физический полная средняя мощности стационарности производства.

Следовательно: D(x)=R_xx(o)-R_xx()

III В силу независимости функции распределения плотности вероятности стационарного процесса от начала отсчета времени КРФ – четная функция.

IV КРФ = max при

Доказательство

Так как средние значение квадратной суммы не может быть <0, то

Примеры 1) Rмонотонно 2) немонотонно

R() R(t)

m_x² t

На практике вместо СП x(t). Рассматривается его отклонение от математического ожидания:

[пульсации или флюктуаций процесса] КРФ:

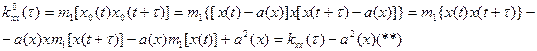
Математические отношение =0, а 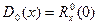отклонение норма (коэффициентов корреляции) пульсаций стационарного процесса.

Примеры

r⁰(t) r⁰(t)

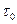
Для чисто стационарного случайного процесса всегда можно указать значение , что при величины 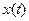и можно считать независимым, причем практический независимость понимается в сигнале, что при интервале 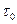называют временем корреляции стационарного процесса. Время корреляций определяется как половина, ширины прямоугольника единицы высоты, площадь которого равна площади под градиентом коэффициента корреляций

Дата добавления: 2014-01-13