Модуль Юнга дорівнює напрузі, при якій відносне видовження дорівнює одиниці

При малих деформаціях пружна напруга пропорційна відносній деформації.

Фізичний зміст модуля Юнга полягає в наступному:

Приведемо (3.3) до виду (3.1):

;	;	;
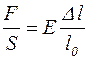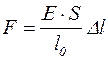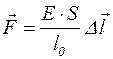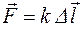,	де	(3.4)

Під час поздовжнього розтягу стержня його поперечний переріз S зменшується. Відносний поперечний стиск ( або коефіцієнт поперечного стиску) дорівнює:

, де d − діаметр стержня.

Дослід показує, що для всіх тіл з одного й того ж матеріалу відношення коефіцієнта поперечного стиску ε_п до відносного видовження ε є величина стала: . Коефіцієнт μ називають коефіцієнтом Пуассона або модулем поперечногостиску.

Застосуємо закон Гука до деформації зсуву. Візьмемо куб з однорідної ізотропної речовини, нижню грань якого закріплено нерухомо. Подіємо на верхню грань дотичною силою f, рівномірно

розподіленою по площі верхньої грані. Дія сили приведе до деформації зсуву і бічна грань ABCD перетвориться в ромб AB'C'D (див. рис. 3.2). Зсув шарів, паралельних верхній грані, відносно нижнього шару характеризують кутом зсуву γ; при малих кутах γ:

.

Відношення тангенціальної розподіленої сили f до площі грані S називають тангенціальною напругою :

.

Закон Гука для деформації зсуву можна записати у виді:

,

(3.5)

де G – коефіцієнт пропорціональності, який називають модулем зсуву.

Між модулем Юнга, коефіцієнтом Пуассона та модулем зсуву існує зв'язок, який описується виразом (3.6):

(3.6)

Межі застосування закону Гука ілюструються графіком залежності від 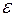(рис.3.3).

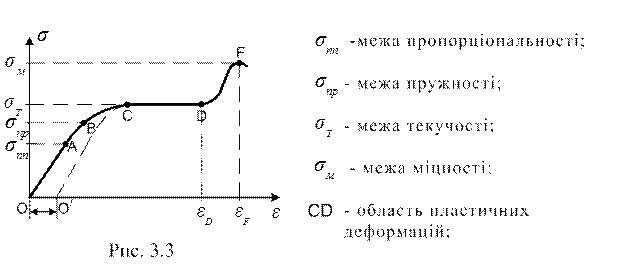
Для всіх напруг, які перевищують межу пружності 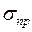, виникають деформації, що залишаються після припинення дії зовнішніх сил (ОО^/ на рис.3.3). Їх називають залишковими або пластичними деформаціями. При деформаціях, більших 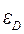, пружні сили знову трохи зростають, а при деформації, що перевищує 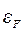, наступає розрив зразка.

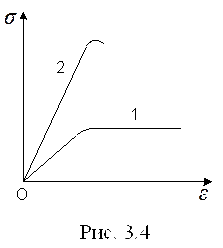Матеріали, що мають значну область текучості CD, називають пластичними або в’язкими (графік 1 на рис.3.4); матеріали, в яких ця область практично відсутня (графік 2), називають крихкими. В реальних твердих тілах деформація досягає певного значення не одразу після початку дії сили, а лише через деякий час. Так само після припинення дії зовнішньої сили деформація зникає не миттєво: спочатку вона швидко зменшується до деякої малої величини, а потім зникає досить повільно. Це явище дістало назву пружної післядії.

Розглянемо ще одне явище, пов’язане з наявністю залишкової деформації. Візьмемо недеформований зразок і будемо його розтягувати; зміна σ від ε для нього зображається кривою OA на рис.3.5. Потім зменшуватимемо напругу до нуля; графік піде нижче кривої OA; зразок прийде в стан B, що характеризується залишковою деформацією ОВ. Щоб її знищити, треба стиснути тіло (тобто, прикласти від’ємну напругу OC). Якщо продовжити стиск далі, то залежність σ (ε) піде по кривій CD. Знову зменшимо напругу до нуля – крива DF. В зразку в положенні F є остаточна деформація стиску FO. Щоб її позбутися, слід розтягнути зразок (напруга OM). Подальший розтяг приведе нас знову в точку A. Одержана петля ABCDFMA має назву петлі пружного гістерезису. Явище пружного гістерезису полягає у відставанні деформації від зміни напруги.

Дата добавления: 2014-01-11