Общий план исследования функций и построение графиков

1.

a. Найти ОДЗ и точки разрыва функции.

b. Найти точки пересечения графика функции с осями координат.

2. Провести исследование функции с помощью первой производной, то есть найти точки экстремума функции и интервалы возрастания и убывания.

3. Исследовать функцию с помощью производной второго порядка, то есть найти точки перегиба графика функции и интервалы его выпуклости и вогнутости.

4. Найти асимптоты графика функции: а) вертикальные, b) наклонные.

5. На основании проведенного исследования построить график функции.

Заметим, что перед построением графика полезно установить, не является ли данная функция четной или нечетной.

Вспомним, что функция называется четной, если при изменении знака аргумента значение функции не меняется: f(-x) = f(x) и функция называется нечетной, если f(-x) = -f(x).

В этом случае достаточно исследовать функцию и построить её график при положительных значениях аргумента, принадлежащих ОДЗ. При отрицательных значениях аргумента график достраивается на том основании, что для четной функции он симметричен относительно оси Oy, а для нечетной относительно начала координат.

Примеры. Исследовать функции и построить их графики.

1. .

1. Область определения функции D(у)= (–∞; +∞). Точек разрыва нет.

Пересечение с осью Ox: x = 0, у= 0.

Функция нечетная, следовательно, можно исследовать ее только на промежутке [0, +∞).

2. . Критические точки: x₁ = 1; x₂ = –1.

3.

3.

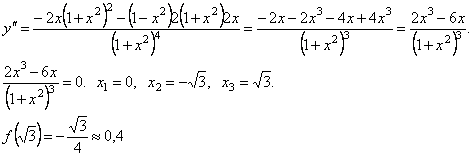
4. а) Вертикальных асимптот нет

б) .

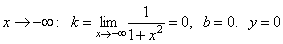
Асимптота – y = 0.

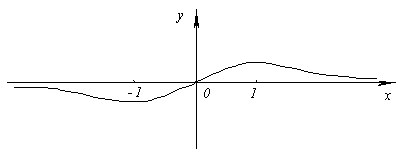
2. .

1. D(y)= (–∞; +∞). Точек разрыва нет.

Пересечение с осью Ox: .

2.

3. .

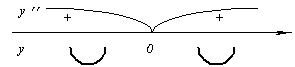
4. а) Вертикальных асимптот нет

б).

Наклонных асимптот нет.

3. .

1. D(y)= (0; +∞). Функция непрерывна на области определения.

Пересечение с осью :

2.

3.

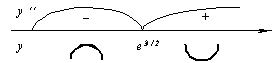
4. а) .

Вертикальная асимптота x = 0.

б).

Наклонная асимптота y = 0.

5. .

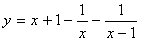1. D(y)= (–∞;0)È(0;1)È(1;+∞).

Функция имеет две точки разрыва x = 0 и x = 1.

Точек пересечения с осями координат нет.

2. при любых действительных значениях x. Поэтому функция возрастает на всей числовой прямой.

3.

4. а)

Вертикальные асимптоты x = 0, x = 1.

б)

Наклонная асимптота y = x + 1.

Раздел VI. Комплексные числа

Дата добавления: 2014-01-13