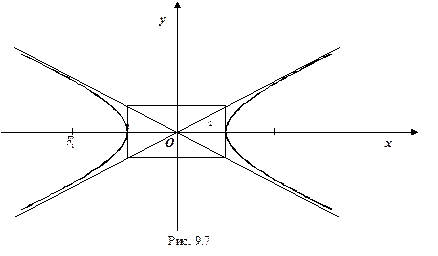КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Гипербола
|
|
|
|
Эллипс
Эллипсом называется линия, состоящая из всех точек плоскости, для каждой из которых сумма расстояний до двух данных точек 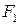 и
и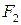 есть величина постоянная (большая, чем расстояние между
есть величина постоянная (большая, чем расстояние между 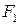 и
и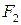 ).
).
Точки 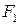 и
и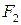 называются фокусами эллипса. Обозначив расстояние между фокусами через
называются фокусами эллипса. Обозначив расстояние между фокусами через 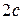 , а сумму расстояний от точек эллипса до фокусов через
, а сумму расстояний от точек эллипса до фокусов через 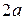 , имеем
, имеем 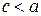 . Если это условие не выполнено, то рассматриваемое множество точек либо отрезок прямой, заключенной между фокусами, либо не содержит ни одной точки.
. Если это условие не выполнено, то рассматриваемое множество точек либо отрезок прямой, заключенной между фокусами, либо не содержит ни одной точки.
Из определения эллипса вытекает следующий метод его построения: если концы нерастяжимой нити длины 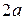 закрепить в точках
закрепить в точках 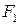 и
и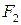 и натянуть нить острием карандаша, то при движении острия будет вычерчиваться эллипс с фокусами
и натянуть нить острием карандаша, то при движении острия будет вычерчиваться эллипс с фокусами 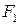 и
и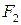 и с суммой расстояний от произвольной точки эллипса до фокусов, равной
и с суммой расстояний от произвольной точки эллипса до фокусов, равной 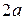 (Рис. 7.1).
(Рис. 7.1).
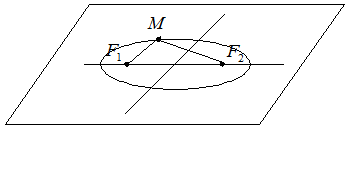
Рис. 7.1
Составим уравнение эллипса. Для этой цели расположим декартову прямоугольную систему координат таким образом, чтобы ось 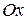 походила через фокусы
походила через фокусы 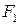 и
и 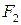 , положительное направление оси – от
, положительное направление оси – от 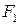 к
к 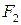 , начало координат выберем в середине отрезка
, начало координат выберем в середине отрезка 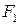
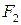 . Тогда координаты точек
. Тогда координаты точек 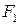 и
и 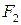 будут соответственно
будут соответственно 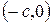 и
и 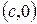 .
.
Пусть 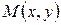 ‑ произвольная точка эллипса, тогда
‑ произвольная точка эллипса, тогда
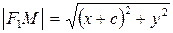 ,
,
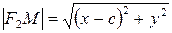 .
.
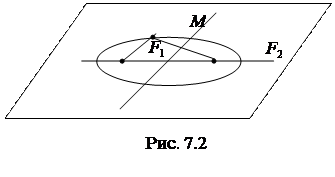
По определению эллипса 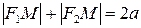 . Подставляя сюда значения
. Подставляя сюда значения 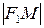 и
и 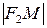 , имеем
, имеем
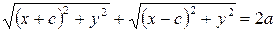 . .
| (7.1) |
Уравнение (1) и есть уравнение эллипса. Преобразуя, упростим его:
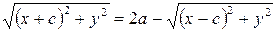 .
.
Возведя обе части уравнения в квадрат и приведя подобные члены, получим: 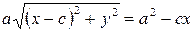 .
.
Возведем еще раз обе части в квадрат и приведем подобные члены. Получаем 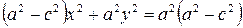 или
или
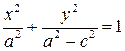
| (7.2) |
Положительную величину 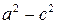 обозначим через
обозначим через 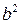 . Тогда уравнение (7.2) примет вид:
. Тогда уравнение (7.2) примет вид:
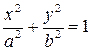
| (7.3) |
Оно называется каноническим уравнение эллипса.
Координаты точек эллипса ограничены неравенствами 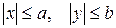 . Значит, эллипс ограниченная фигура, не выходящая за пределы прямоугольника со сторонами
. Значит, эллипс ограниченная фигура, не выходящая за пределы прямоугольника со сторонами 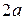 и
и 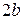
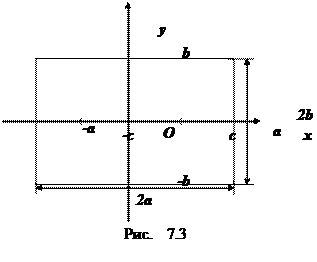
Заметим, что в уравнение (7.3) входят лишь четные степени 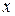 и
и 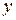 . Поэтому, если точка
. Поэтому, если точка 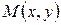 принадлежит эллипсу, то и точки
принадлежит эллипсу, то и точки 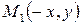 ,
, 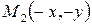 ,
, 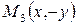 также ему принадлежат. А это означает, что эллипс – линия симметричная относительно координатных осей
также ему принадлежат. А это означает, что эллипс – линия симметричная относительно координатных осей 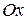 и
и  .
.
Поэтому для исследования формы эллипса достаточно рассмотреть его в первой координатной четверти, а в остальных четвертях его строение определяется по симметрии. Для первой четверти, из уравнения (7.3) имеем
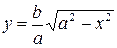
| (7.4) |
При возрастании 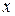 от
от 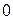 до
до 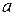 ,
, 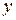 монотонно убывает от
монотонно убывает от 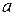 до
до 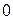 . График функции изображен на Рис. 7.4.
. График функции изображен на Рис. 7.4.
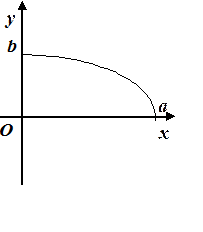
Рис. 7.4
Достроив остальные четверти эллипса по симметрии, получим весь эллипс (Рис. 7.5).
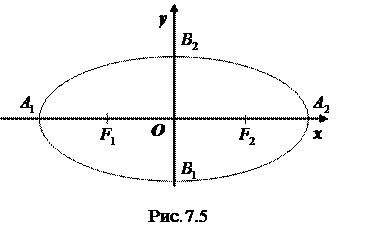
Оси симметрии эллипса (оси 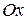 и
и  ) называются просто его осями, а центр симметрии – точка
) называются просто его осями, а центр симметрии – точка 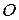 ‑ центром эллипса. Точки
‑ центром эллипса. Точки 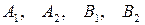 пересечения эллипса с осями координат называются вершинами эллипса. Отрезки
пересечения эллипса с осями координат называются вершинами эллипса. Отрезки 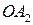 и
и 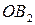 , а также их длины
, а также их длины 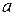 и
и 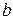 называются полуосями эллипса. В случае, когда фокусы эллипса находятся на оси
называются полуосями эллипса. В случае, когда фокусы эллипса находятся на оси 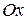 (как в нашем случае), из равенства
(как в нашем случае), из равенства 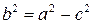 , следует, что
, следует, что 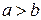 . В этом случае
. В этом случае 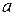 называется большой полуосью, а
называется большой полуосью, а 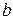 ‑ малой.
‑ малой.
Если 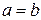 , то уравнение (7.3) можно переписать в виде:
, то уравнение (7.3) можно переписать в виде:
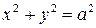
| (7.5) |
Это уравнение окружности с центром в начале координат. Эллипс (3) можно получить из окружности (4) сжатием плоскости к оси 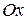 . Пусть на плоскости выбрана прямоугольная система координат
. Пусть на плоскости выбрана прямоугольная система координат 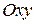 . Тогда преобразование, переводящее произвольную точку
. Тогда преобразование, переводящее произвольную точку 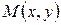 в точку
в точку 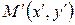 , координаты которой задаются формулами
, координаты которой задаются формулами 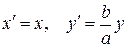 , будет окружность (4) переводить в эллипс, заданный соотношением
, будет окружность (4) переводить в эллипс, заданный соотношением 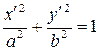 .
.
Число 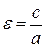 называется эксцентриситетом эллипса. Эксцентриситет
называется эксцентриситетом эллипса. Эксцентриситет 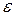 характеризует форму эллипса: чем ближе к нулю, тем больше эллипс похож на окружность; при увеличении
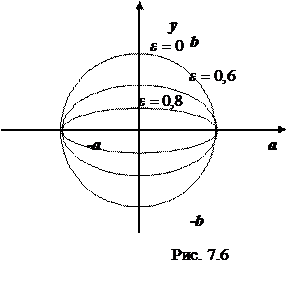
характеризует форму эллипса: чем ближе к нулю, тем больше эллипс похож на окружность; при увеличении 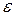 становится более вытянутым (Рис. 7.6).
становится более вытянутым (Рис. 7.6).
Фокальными радиусами точки 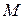 эллипса называются отрезки прямых, соединяющие эту точку с фокусами
эллипса называются отрезки прямых, соединяющие эту точку с фокусами 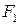 и
и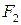 . Их длины
. Их длины 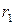 и
и 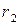 задаются формулами
задаются формулами 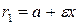 и
и 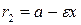 . Прямые
. Прямые 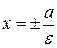 называются директрисами эллипса. Директриса
называются директрисами эллипса. Директриса 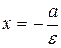 называется левой, а
называется левой, а 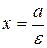 ‑ правой. Так как для эллипса
‑ правой. Так как для эллипса 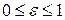 , то
, то 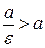 и, следовательно, левая директриса располагается левее левой вершины эллипса, а правая – правее правой вершины.
и, следовательно, левая директриса располагается левее левой вершины эллипса, а правая – правее правой вершины.
Директрисы обладают следующим свойством: отношение расстояния 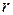 любой точки эллипса от фокуса к ее расстоянию
любой точки эллипса от фокуса к ее расстоянию 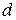 до соответствующей директрисы есть величина постоянная, равная эксцентриситету, т.е.
до соответствующей директрисы есть величина постоянная, равная эксцентриситету, т.е. 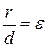 .
.
Гиперболой называется линия, состоящая из всех точек плоскости, модуль разности расстояний от которых до двух данных точек 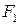 и
и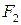 есть величина постоянная (не равная нулю и меньшая, чем расстояние между
есть величина постоянная (не равная нулю и меньшая, чем расстояние между 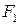 и
и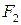 ).
).
Точки 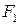 и
и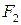 называются фокусами гиперболы. Пусть по-прежнему расстояние между фокусами равно
называются фокусами гиперболы. Пусть по-прежнему расстояние между фокусами равно 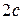 . Модуль расстояний от точек гиперболы до фокусов
. Модуль расстояний от точек гиперболы до фокусов 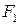 и
и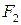 обозначим через
обозначим через 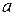 . По условию,
. По условию, 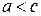 .
.
Выбрав декартову систему координат, как в случае эллипса, и используя определение гиперболы, составляем ее уравнение:
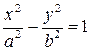
| (7.6) |
где 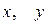 ‑ координаты произвольной точки гиперболы,
‑ координаты произвольной точки гиперболы, 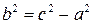 .
.
Уравнение (7.6) называется каноническим уравнением гиперболы.
Из уравнения (7.6) видно, что 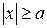 . Это означает, что вся гипербола располагается вне полосы, ограниченной прямыми
. Это означает, что вся гипербола располагается вне полосы, ограниченной прямыми 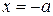 и
и 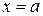 .
.
Так как в уравнение входят только четные степени 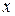 и
и 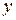 , то гипербола симметрична относительно каждой из координатных осей и начала координат. Поэтому достаточно построить эту кривую в первой четверти: в остальных четвертях гипербола строится по симметрии. Из уравнения (7.6) для первой четверти, имеем:
, то гипербола симметрична относительно каждой из координатных осей и начала координат. Поэтому достаточно построить эту кривую в первой четверти: в остальных четвертях гипербола строится по симметрии. Из уравнения (7.6) для первой четверти, имеем: 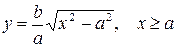 .
.
График этой функции от точки 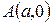 уходит неограниченно вправо и вверх (Рис. 7.7), и как угодно близко подходит к прямой
уходит неограниченно вправо и вверх (Рис. 7.7), и как угодно близко подходит к прямой
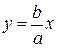
| (7.7) |
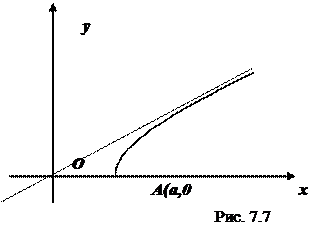
Поэтому говорят, что гипербола асимптоматически приближается к прямой (7.7), и эту прямую называют асимптотой гиперболы. Из симметрии гиперболы следует, что у нее две асимптоты 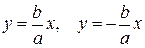 .
.
Построим гиперболу. Сначала строим, так называемый, основной прямоугольник гиперболы, центр которой совпадает с началом координат, а стороны равны 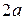 и
и 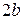 параллельны осям координат. Прямые, на которых расположены диагонали этого прямоугольника, являются асимптотами гиперболы. Сделаем рисунок гиперболы (Рис. 7.8).
параллельны осям координат. Прямые, на которых расположены диагонали этого прямоугольника, являются асимптотами гиперболы. Сделаем рисунок гиперболы (Рис. 7.8).

|

Рис 7.8.
 Гипербола состоит из двух отдельных ветвей. Центр симметрии гиперболы называется ее центром, оси симметрии называются осями гиперболы. Точки
Гипербола состоит из двух отдельных ветвей. Центр симметрии гиперболы называется ее центром, оси симметрии называются осями гиперболы. Точки 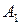 и
и 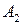 пересечения гиперболы с осью
пересечения гиперболы с осью 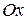 называются вершинами гиперболы. Величины
называются вершинами гиперболы. Величины 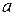 и
и 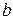 называются полуосями гиперболы. Если
называются полуосями гиперболы. Если 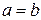 , то гипербола называется равносторонней.
, то гипербола называется равносторонней.
Эксцентриситетом гиперболы называется число 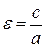 . Для любой гиперболы
. Для любой гиперболы 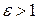 . Эксцентриситет характеризует форму гиперболы: чем меньше, тем больше вытягивается гипербола вдоль оси
. Эксцентриситет характеризует форму гиперболы: чем меньше, тем больше вытягивается гипербола вдоль оси 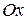 . На Рис. 7.9 изображены гиперболы с различными значениями
. На Рис. 7.9 изображены гиперболы с различными значениями 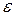 .
.

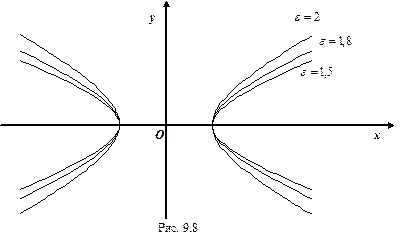
Рис. 7.9
Фокальными радиусами точки гиперболы называются отрезки прямых, соединяющие эту точку с фокусами 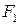 и
и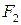 . Их длины
. Их длины 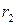 и
и 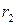 задаются формулами:
задаются формулами:
Для правой ветви 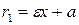 ,
,
Для левой ветви 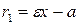 .
.
Прямые 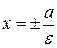 называются директрисами гиперболы. Как и в случае эллипса, точки гиперболы характеризуются соотношением
называются директрисами гиперболы. Как и в случае эллипса, точки гиперболы характеризуются соотношением 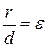 .
.
|
|
|
|
|
Дата добавления: 2014-01-13; Просмотров: 576; Нарушение авторских прав?; Мы поможем в написании вашей работы!