Исследование на плоскости уравнения второй степени

Рассмотрим уравнение

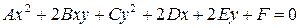
(7.9)

где среди коэффициентов есть отличные от нуля, т.е. (7.9) – уравнение второй степени относительно 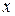и .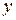

Возьмем на плоскости две прямоугольные системы координат: 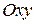, которую будем называть старой, и новую, полученную из 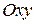поворотом ее вокруг начала координат на угол , .

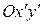Старые координаты 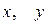выражаются через новые координаты 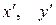по формулам:

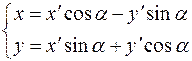
(7.10)

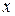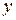Подставив выражения для и в уравнение (8), получим

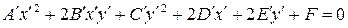
(7.11)

Это уравнение в системе координат 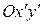задает ту же линию, что и уравнение (7. 9) в системе .

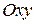Если в уравнении (7.9) 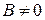, то за счет выбора угла в (7.10) можно добиться того, что 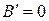. Для этого угол надо взять таким, чтобы 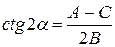. Поэтому будем считать 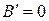, тогда уравнение (7.11) примет вид:

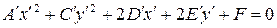
(7.12)

Преобразуя это уравнение и применяя параллельный перенос координатных осей, придем к уравнению

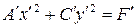
(7.13)

В зависимости от знаков коэффициентов уравнения (7.13) рассмотрим следующие случаи:

I 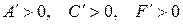, тогда уравнение (7.13) примет вид 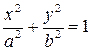, где 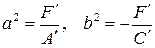. это уравнение эллипса.

II 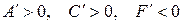, то обозначив 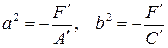имеем 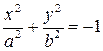. Этому уравнению не удовлетворяет ни одна точка с координатами 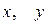. Следовательно, это уравнение задает пустое множество.

III 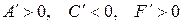. Обозначая 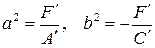приведем уравнение (12) к виду .

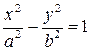Это уравнение гиперболы.

Случаи 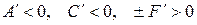, , 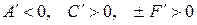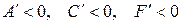новых результатов не дают.

IV 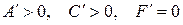. Тогда уравнение (7.13) можно привести к виду 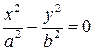. Это уравнение задает пару прямых 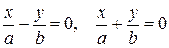, пересекающихся в начале координат.

Рассматривая далее методично все случаи, придем к выводу: уравнение вида (7.9) задает одну из следующих фигур: эллипс, гиперболу, параболу, пару пересекающихся прямых, пару параллельных прямых, прямую, точку или пустое множество.

Контрольные вопросы к теме

1. Понятие кривых второго порядка: эллипса, гиперболы, параболы.

2. Уравнение эллипса, каноническое уравнение эллипса.

3. Понятия фокусов эллипса; фокальных радиусов; директрисы иэксцентриситета эллипса.

4. Каноническое уравнение гиперболы.

5. Фокусы и фокальныерадиусыгиперболы, асимптота гиперболы.

6. Каноническое уравнение параболы.

7. Приведение уравнения второй степени к каноническому виду.

Дата добавления: 2014-01-13