Метод наименьших квадратов

При определении вида эмпирической функции 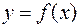обычно предполагается, что это наиболее гладкая кривая, согласованная с экспериментальными данными. Кроме того, для выбора этой функции привлекаются дополнительные соображения, как правило, не математического характера (теоретические модели, опыт предшествующих исследований, и т.п.).

Эта задача может быть решена в ходе регрессионного анализа, который изучается в курсе теории вероятностей, но решить ее можно и математическими методами. Согласно наиболее распространенному и теоретически обоснованному методу наименьших квадратов в качестве неизвестных параметров функции 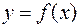выбираются такие значения, которые соответствуют минимальному значению суммы квадратов отклонений эмпирических значений 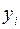от значений функции 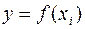вычисленных по соответствующим им значениям аргументов 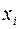, т.е.

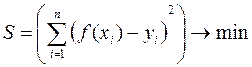
Разность 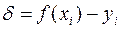называется невязкой. В качестве критерия согласия или величины отклонения можно было взять обычную сумму невязок или их абсолютных величин, но делать это нецелесообразно, поскольку в первом случае сумма невязок может быть малой или, даже, равняться нулю при значительном разбросе экспериментальных данных из-за того, что положительные отклонения будут скомпенсированы отрицательными. Сумма абсолютных величин невязок лишена этого недостатка, но она имеет другой – она не является дифференцируемой, что существенно затрудняет решение задачи.

В ходе решения задачи отыскания оптимальных параметров аппроксимационной функции 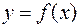возникает необходимость поиска экстремума функции нескольких переменных, поэтому прежде чем решать эту задачу для конкретных эмпирических функций, необходимо рассмотреть свойства функций нескольких переменных.

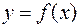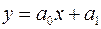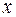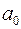Предположим, что функция – линейная, т.е. . Если это выражение приближенно описывает зависимость между и , то сумма квадратов невязок должна быть минимальной, т.е. значения параметров и 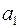должны соответствовать минимуму величины

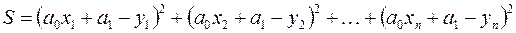
Это функция двух переменных 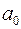и 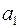, она непрерывна, дифференцируема, неотрицательна и ограничена снизу. Для того чтобы найти ее наименьшее значение, необходимо ее частные производные приравнять к нулю:

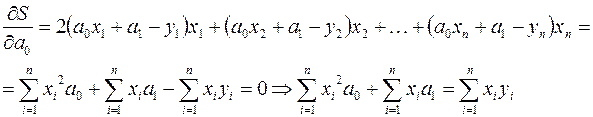
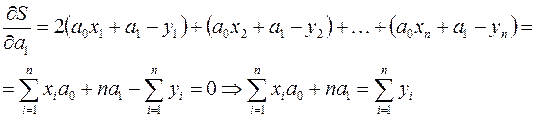
Таким образом, для нахождения параметров 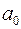и 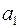необходимо решить систему уравнений:

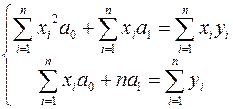
Эта линейная система уравнений имеет единственное решение, поскольку ее определитель 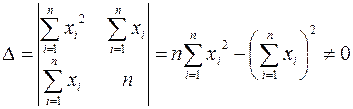не равен нулю.

Вторые производные функции 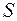равны:

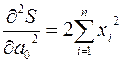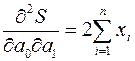; ; . Главные миноры матрицы квадратичной формы положительны, т.е.

;

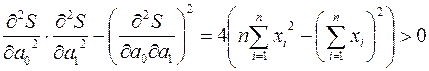. Таким образом, значения 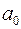и 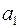, найденные при решении системы уравнений, соответствуют минимуму функции .

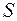Поскольку система невырождена, то решение можно найти по правилу Крамера:

, .

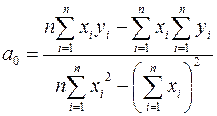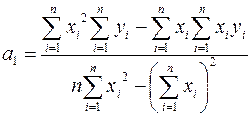Контрольные вопросы к теме

22. Понятия точки и расстояния.

23. Внешняя точка, внутренняя точка и граничная точка. Понятия открытой области и замкнутого множества.

24. Ограниченность и сходимость последовательности точек.

25. Понятия непрерывности и дифференцируемости функций многих переменных.

26. Частные приращения и частные производные.

27. Полный дифференциал функции. Формула Тейлора.

28. Локальный экстремум, условный экстремум. Понятия стационарных и критических точек.

29. Метод наименьших квадратов.

Дата добавления: 2014-01-13