Понятие неопределенного интеграла

Тема 5. Неопределенный интеграл

Основные понятия, включенные в систему тренинг-тестирования:

интегрирование; первообразная; неопределенный интеграл; метод замены переменных; метод интегрирования по частям; метод рационализации.

Интегрирование ­– операция, обратная дифференцированию, которая позволяет определять функцию 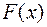, для которой заданная функция является ее производной:

.

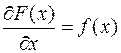Другими словами, если операция дифференцирования состоит в нахождении производной, то интегрирование – это операция отыскания первообразной.

Функция 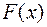называется первообразной для функции , на промежутке 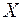, если для каждой точки этого промежутка .

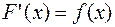Теорема. Есл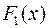ии 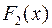– любые две первообразные для данной функции на промежутке 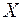, то для всех выполняется равенство .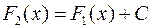

Доказательство: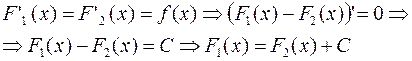

Таким образом, все семейство первообразных для данной функции имеет вид 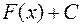, где 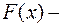одна из первообразных, а 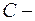произвольная постоянная.

Совокупность всех первообразных для функции на промежутке 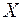называется неопределенным интегралом функции .

Неопределенный интеграл обозначается следующим образом:

,

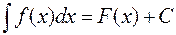где 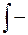знак интеграла;

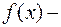подынтегральная функция;

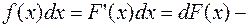подынтегральное выражение.

В определении неопределенного интеграла не исключается возможность того, что подынтегральная функция является сложной, однако при проверке правильности нахождения первообразной это несущественно, поскольку дифференцировать следует лишь по переменной, стоящей под знаком дифференциала.

Можно показать, что достаточным условием интегрируемости функции на промежутке 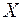является ее непрерывность, в то время как для ее дифференцируемости непрерывность является лишь необходимым условием, но не достаточным.

Дата добавления: 2014-01-13