Понятие о рядах Фурье непериодических функций

Кусочно-дифференцируемую непериодическую функцию , заданную на бесконечной оси 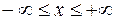, нельзя представить ее рядом Фурье, так как его сумма, будучи суммой гармоник с общим периодом 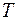, есть функция периодическая с тем же периодом и, следовательно, не может быть равен функции для всех 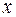. Однако можно построить представление этой функции в виде соответствующего ряда Фурье на любом конечном промежутке.

Пусть интересующий промежуток есть , т.е. симметричен относительно начала координат (этого всегда можно добиться параллельным сдвигом оси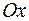

Построим функцию периода 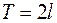такую, что при .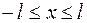

Предполагая, что функция удовлетворяет условиям теоремы о сходимости, имеем:

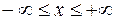, где коэффициенты 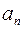и определяются по формулам

.

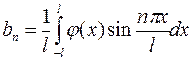Отсюда на основании тождества получим

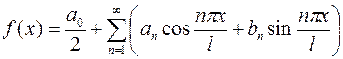
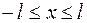, где

.

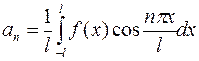
Теперь необходимо подсчитать сумму ряда на концевых точках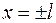

Согласно общей формуле

На основании тождества между и , а также периодичности функции очевидно, что ,

Таким образом, получается, что

.

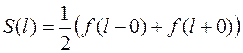Из периодичности функции 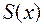следует, что .

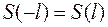Пусть теперь необходимо непериодическую функцию представить в виде ряда Фурье периода 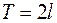на полупериоде

Полагая

где 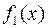– произвольная кусочно – дифференцируемая функция, получаем бесконечное множество рядов Фурье

, ()

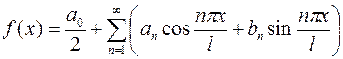дающих представление функции на интервале .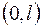

В частности, полагая, что (), т.е. что функция – четная, получим

, ()

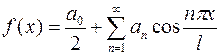где

.

Аналогично, полагая, что (), т.е. что функция – нечетная, получим

,

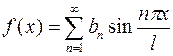где

.

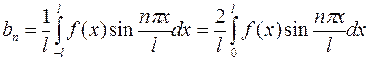
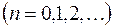Таким образом, кусочно – дифференцируемую функцию, заданную на полупериоде, можно разложить в соответствующий ряд Фурье бесчисленным множеством способов. В частности, по желанию эту функцию на данном полупериоде можно представить в виде суммы четных гармоник или в виде суммы нечетных гармоник.

Контрольные вопросы к теме

1. Понятия числового ряда и его сходимости.
2. Признаки сходимости ряда. Геометрический и гармонический ряды.
3. Знакопеременные и знакочередующиеся ряды, их сходимость и абсолютная сходимость.
4. Область сходимости функционального ряда. Понятие равномерной сходимости ряда.
5. Радиус сходимости степенного ряда, основные методы его определения.
6. Ряд Тейлора. Разложение функций в ряд Тейлора.
7. Понятие кусочно-дифференцируемой функции.
8. Понятие ортогональности функций.
9. Ряд Фурье. Понятие гармонического анализа

Дата добавления: 2014-01-13