
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Движение материальной точки по окружности. Угловая скорость. Угловое ускорение
|
|
|
|
Движение материальной. точки по окружности является частным случаем криволинейного движения.
При движении точки по окружности вектор линейной скорости ее  (рис.5.1) непрерывно изменяет свое направление, при этом радиус-вектор ее
(рис.5.1) непрерывно изменяет свое направление, при этом радиус-вектор ее 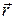 непрерывно поворачивается. За промежуток времени Dt он поворачивается на угол D j. Нужно указать, в какую сторону происходит этот поворот (по часовой стрелке или против). Таким образом, возникает необходимость считать угол поворота радиус-вектора величиной векторной. Длина вектора Δ φ равна величине угла поворота Δφ, а направление совпадает с осью, вокруг которой производится поворот.
непрерывно поворачивается. За промежуток времени Dt он поворачивается на угол D j. Нужно указать, в какую сторону происходит этот поворот (по часовой стрелке или против). Таким образом, возникает необходимость считать угол поворота радиус-вектора величиной векторной. Длина вектора Δ φ равна величине угла поворота Δφ, а направление совпадает с осью, вокруг которой производится поворот.

Если величина угла D j очень мала (по сравнению с p радиан), то направление вектора 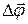 выбирают так: он направлен по оси, в которой она лежит, в сторону поступательного движения буравчика, ручка которого вращается в направлении движения материальной точки (рис.5.1)
выбирают так: он направлен по оси, в которой она лежит, в сторону поступательного движения буравчика, ручка которого вращается в направлении движения материальной точки (рис.5.1)
По аналогии со скоростью поступательного движения введем вектор угловой скорости  .
.
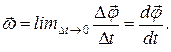 (5.1)
(5.1)
Вектор  направлен так же, как и вектор
направлен так же, как и вектор 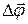 . Вектор линейной скорости
. Вектор линейной скорости  точки определяется так:
точки определяется так:
 (5.2)
(5.2)
Если учесть, что 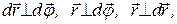 то
то 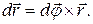
Поэтому
 (5.3)
(5.3)
Если угловая скорость не меняется с течением времени, то движение часто называют «равномерным движением по окружности». Однако в этом случае подразумевают только тот факт, что скорость точки при движении не меняется по величине. На самом же деле это движение ускоренное, так как в каждый последующий момент времени меняется направление скорости, т. е. движущееся тело имеет ускорение 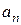 . По величине это ускорение, согласно (3.6), равно
. По величине это ускорение, согласно (3.6), равно 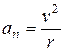 и направлено по радиусу к центру, поэтому нормальное ускорение часто называют центростремительным.
и направлено по радиусу к центру, поэтому нормальное ускорение часто называют центростремительным.
|
|
|
Если точка при движении с постоянной скоростью по окружности за время  переместилась на
переместилась на 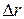 , то величина скорости равна:
, то величина скорости равна:
 (5.4)
(5.4)
Это соотношение указывает на связь между линейной и угловой скоростями.
Если угловая скорость постоянна, то движение равномерное и его можно характеризовать периодом вращения Т – временем, за которое точка совершает один полный оборот, т.е. поворачивается на угол 2π. Т.к. промежутку времени Δt=T соответствует Δφ=2π, то ω=2π/Т, откуда
Т = 2π/ω (5.5)
Число полных оборотов, совершаемых телом в единицу времени, называется частотой вращения n:
n=1/T= ω/(2π) (5.6)
Отсюда
ω=2 πn (5.7)
Для равномерного движения тела по окружности, если  - начальное угловое положение некоторой точки А, а
- начальное угловое положение некоторой точки А, а  = 0 - начальный момент времени, то
= 0 - начальный момент времени, то
 (5.8)
(5.8)
Если угловая скорость тела меняется со временем, то вводят понятие углового ускорения 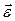 – быстроты изменения угловой скорости:
– быстроты изменения угловой скорости:
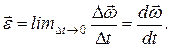 (5.9)
(5.9)

 ω2 ω1
ω2 ω1


 ω1
ω1 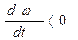 ω2
ω2


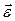
 >0
>0 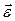 <0
<0
 |
Рис.5.2.
При вращении тела вокруг неподвижной оси вектор углового ускорения направлен вдоль оси вращения в сторону вектора элементарного приращения угловой скорости. При ускоренном движении вектор 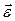 сонаправлен вектору ω, при замедленном – противонаправлен ему (рис. 5.2.)
сонаправлен вектору ω, при замедленном – противонаправлен ему (рис. 5.2.)
Если отсчет времени начинаем с нуля, то
 (5.10)
(5.10)
и
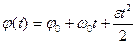 (5.11)
(5.11)
Вектор углового ускорения 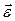 связан с вектором ускорения
связан с вектором ускорения  следующим образом:
следующим образом:
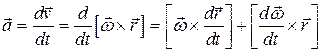 ;
;
 тогда первое слагаемое можно записать
тогда первое слагаемое можно записать 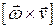 , но
, но  и получаем
и получаем  - это так называемое двойное векторное произведение. Его можно расписать следующим образом:
- это так называемое двойное векторное произведение. Его можно расписать следующим образом:

так как  и их скалярное произведение равно 0.
и их скалярное произведение равно 0.
 - по определению. В итоге получаем
- по определению. В итоге получаем
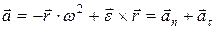 .
.
Первое слагаемое 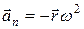 нормальное ускорение имеет знак минус, так как
нормальное ускорение имеет знак минус, так как 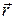 и
и  противоположно направлены. Второе слагаемое
противоположно направлены. Второе слагаемое 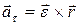 - тангенциальное ускорение.
- тангенциальное ускорение.
Пример. Маховое колесо, вращающееся со скоростью п об/с, останавливается в течение  секунд. Считая движение равнозамедленным, определить, сколько оборотов N оно сделало до полной остановки.
секунд. Считая движение равнозамедленным, определить, сколько оборотов N оно сделало до полной остановки.
|
|
|
Маховое колесо движется замедленно с постоянным угловым ускорением  , величина которого в условии не задана. Угловая скорость колеса в каждый момент времени определяется формулой
, величина которого в условии не задана. Угловая скорость колеса в каждый момент времени определяется формулой  . Так как через
. Так как через  секунд колесо останавливается, то
секунд колесо останавливается, то  . Отсюда
. Отсюда
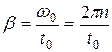 .
.
Полный угол 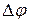 , который описывает любая точка махового колеса с момента торможения до полной остановки, можно определить по формуле (1.59)
, который описывает любая точка махового колеса с момента торможения до полной остановки, можно определить по формуле (1.59)
 |
Поскольку один оборот колеса соответствует углу поворота любой его точки на 2л радиан, то полное число оборотов N колеса до остановки равно
|
|
|
|
Дата добавления: 2014-01-11; Просмотров: 4499; Нарушение авторских прав?; Мы поможем в написании вашей работы!