
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Примеры решения задач
|
|
|
|
В динамике Ньютона природа сил, входящих в основное уравнение движения (6.5), не имеет значения. Важно знать, каковы их модули и направление. Для успешного решения задач с использованием второго закона Ньютона желательно познакомиться с некоторой последовательностью действий (своего рода «алгоритмом»).
1. Так как движение тела определяется всеми действующими на тело силами, то необходимо на рисунке к задаче стрелочками указать все силы, действующие на тело. Очень полезно отчетливо представить, со стороны каких тел действуют рассматриваемые силы.
 |
2. После того как определим все силы, действующие на тело, необходимо второй закон Ньютона записать в векторной форме:
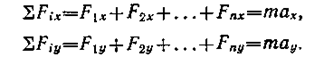 |
Далее нужно выбрать какое-либо удобное направление осей OX и OY (обычно оно диктуется условием задачи) и перейти к уравнениям для проекций на оси координат:
3.Если в задаче кроме сил и ускорений требуется определить координаты и скорости, то кроме уравнений движения нужно использовать еще и кинематические уравнения (1.36) и (1.38).
4.Записав систему уравнений для данной задачи, необходимо проследить за тем, чтобы общее число уравнений равнялось числу неизвестных.
Решение задачи следует получить сначала в общем виде. Это позволит произвести анализ решения, т.е. увидеть, как меняются найденные величины от условия задачи. И только после этого в полученные формулы нужно подставить цифровые данные.
Приведем решение нескольких типичных задач.
Пример 1. На груз действуют две постоянные силы: сила тяжести mg и сила натяжения нити F (рис. 6.1), поэтому он будет двигаться с постоянным ускорением. Запишем второй закон Ньютона для груза: F+mg=ma. Выберем ось координат ОХ направленной вверх (хотя ее можно было бы направить и вниз),
тогда этот закон в проекции на ось ОХ запишется: F—mg=ma. Откуда
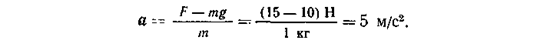 |
Поскольку ускорение получилось положительной величиной, то можно сказать, что ускорение лифта направлено вверх. О направлении движения лифта ничего сказать нельзя, так как о направлении движения тела можно судить только по направлению скорости, а не ускорения. Скорость в каждый момент времени определяется формулой: 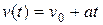 . Поэтому, чтобы ответить на вопрос, куда движется лифт, нужно знать его начальную скорость v
. Поэтому, чтобы ответить на вопрос, куда движется лифт, нужно знать его начальную скорость v . И только в том случае, когда начальная скорость v
. И только в том случае, когда начальная скорость v равна нулю, направление движения тела определяется направлением ускорения.
равна нулю, направление движения тела определяется направлением ускорения.
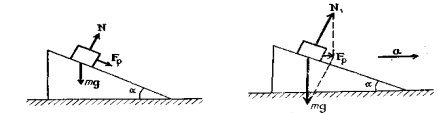 |
Пример 2. На гладкой наклонной плоскости, образующей угол
 с горизонтом, находится тело массой
с горизонтом, находится тело массой  . Найти ускорение тела а, реакцию опоры N и результирующую силу F
. Найти ускорение тела а, реакцию опоры N и результирующую силу F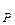 .
.
| Рис.6.2. | Рис.6.3. |
На тело действуют две силы: сила тяжести mg и реакция опоры N. Результирующая этих сил F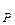 заставляет тело двигаться вдоль наклонной плоскости с ускорением а (рис. 2.2). Тогда
заставляет тело двигаться вдоль наклонной плоскости с ускорением а (рис. 2.2). Тогда
N + mg = ma.
 |
Так как тело перемещается по наклонной плоскости, то ось ох направим вдоль наклонной плоскости вниз, а ось оу — перпендикулярно к ней. Тогда уравнение движения в проекциях на эти оси запишется
Следовательно, a=gsin , N=mgcos
, N=mgcos , |Fp| = |ma|=mgsin
, |Fp| = |ma|=mgsin  .
.
Изменим немного эту задачу. Пусть тело находится на этой же плоскости, но теперь наклонную плоскость перемещаем с ускорением а по горизонтали так, чтобы тело на ней покоилось. Вновь определим величину и направление результирующей силы F 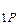 и реакцию опоры N
и реакцию опоры N 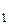 .
.
На тело по-прежнему действуют две силы mg и N. Уравнение движения в
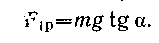 |
векторной форме записывается аналогично: mg+N
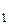 =mа. Тело покоится на наклонной плоскости, но относительно Земли оно вместе с наклонной плоскостью движется с ускорением а. Следовательно, результирующая сила F
=mа. Тело покоится на наклонной плоскости, но относительно Земли оно вместе с наклонной плоскостью движется с ускорением а. Следовательно, результирующая сила F 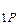 направлена в ту же сторону, что и ускорение а (рис. 2.3). Величину ее легко определить из прямоугольного треугольника.
направлена в ту же сторону, что и ускорение а (рис. 2.3). Величину ее легко определить из прямоугольного треугольника.Сила реакции опоры N 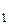 вычисляется из того же треугольника N
вычисляется из того же треугольника N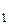 =mg/cos
=mg/cos  . Как видно, силы F
. Как видно, силы F 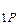 и N
и N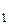 , по величине отличаются от F
, по величине отличаются от F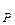 и N.
и N.
Пример 3. Два тела с массами m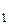 и m
и m 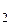 связаны невесомой и нерастяжимой нитью и покоятся на идеально гладкой горизонтальной плоскости. С каким ускорением движутся тела, если к телу массы m
связаны невесомой и нерастяжимой нитью и покоятся на идеально гладкой горизонтальной плоскости. С каким ускорением движутся тела, если к телу массы m 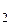 приложена горизонтальная сила F (рис. 6.4).
приложена горизонтальная сила F (рис. 6.4).
Вначале укажем все силы, действующие на тело. На первое тело действуют силы: сила тяжести mg, сила реакции опоры N r сила натяжения нити Т 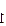 . На второе тело действуют сила: F
. На второе тело действуют сила: F 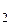 сила тяжести m
сила тяжести m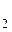 g, сила реакции опоры N
g, сила реакции опоры N 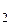 и сила натяжения нити Т
и сила натяжения нити Т 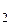 (рис. 6.4, а). Запишем второй закон Ньютона для обоих тел:
(рис. 6.4, а). Запишем второй закон Ньютона для обоих тел:
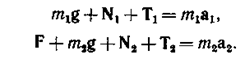 |
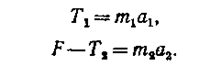 |
Направим ось ОХ вдоль направления силы F и перепишем закон Ньютона в проекциях на эту ось:
Мы получили два уравнения с четырьмя неизвестными, поэтому нужны еще дополнительные уравнения. Одно из них получается из условия нерастяжимости нити. В этом случае оба конца нити за любые промежутки времени совершают равные перемещения, т.е.:
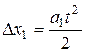 и
и 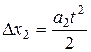
Из этих отношений следует, что 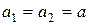 . Условие невесомости нити позволяет найти связь между силами Т
. Условие невесомости нити позволяет найти связь между силами Т 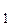 и Т
и Т 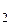 . По третьему закону Ньютона на концы нити действуют силы Т
. По третьему закону Ньютона на концы нити действуют силы Т 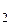 и Т
и Т 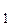 (их направления указаны стрелками, рис. 6.4,6). В проекциях на ось ох для нити можно записать Т
(их направления указаны стрелками, рис. 6.4,6). В проекциях на ось ох для нити можно записать Т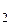 - Т
- Т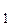 =m
=m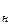 a.
a.
Так как нить невесома, m 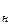 = 0, то Т
= 0, то Т 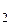 = Т
= Т 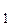 = Т. Таким образом, невесомая нить действует на тело с равными по величине, но противоположными по направлению силами. Это позволяет записать уравнения движения для тел вдоль оси ОХ в виде
= Т. Таким образом, невесомая нить действует на тело с равными по величине, но противоположными по направлению силами. Это позволяет записать уравнения движения для тел вдоль оси ОХ в виде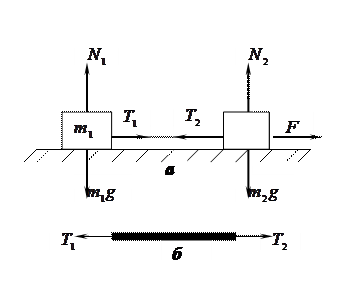
Рис. 6.4.
 |
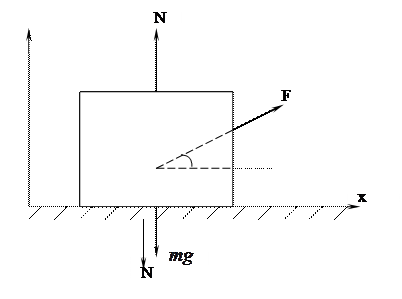
Пример 4. На идеально гладкой горизонтальной поверхности под действием силы F, направленной под углом  к горизонту (рис. 6.5), движется тело массой m. Определить ускорение тела а и силу N ', с которой тело действует на плоскость.
к горизонту (рис. 6.5), движется тело массой m. Определить ускорение тела а и силу N ', с которой тело действует на плоскость.
На тело действуют три силы: сила тяжести m g, сила реакции опоры N и сила F, направленная под углом  к горизонту. Согласно второму закону Ньютона
к горизонту. Согласно второму закону Ньютона
m g + N + F = m a.
Так как тело движется вдоль горизонтальной плоскости, ось OX направим, как показано на рисунке, а ось OY — перпендикулярно ей. Тогда закон Ньютона в проекциях на оси координат запишется:
по оси OX:
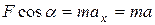 ;
;
по оси OY:
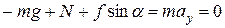
Определим ускорение:
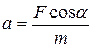 .
.
Сила, с которой тело действует на плоскость (N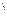 ) по третьему закону Ньютона численно равна силе, с которой плоскость действует на тело ( N), т.е.
) по третьему закону Ньютона численно равна силе, с которой плоскость действует на тело ( N), т.е.
N=- N ', или | N'| = |N|
Силу N легко найти из уравнения движения, записанного вдоль оси OY:
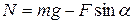
 |
следовательно, |N'|=|N |=
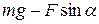 , однако нужно помнить, что эта сила приложена к плоскости.
, однако нужно помнить, что эта сила приложена к плоскости.
Рис. 6.5
Пример 5. Пусть тело движется вдоль стола под действием горизонтальной силы F. На тело действуют четыре силы: сила F, сила тяжести mg, реакция опоры R и сила трения F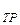 '(рис. 6.6,а). Векторная форма второго закона Ньютона имеет вид
'(рис. 6.6,а). Векторная форма второго закона Ньютона имеет вид
F+ mg+R+F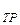 =ma.
=ma.
Согласно третьему закону Ньютона сила нормального давления N равна по модулю, но противоположна по направлению силе реакции со стороны стола R (силе, с которой стол действует на тело), т. е.
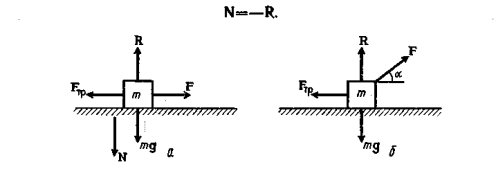 |
Рис.6.6.
Сила реакции стола определяется из второго закона Ньютона: вдоль вертикального направления на тело действуют две силы (сила тяжести mg и сила реакции R). Так как тело не перемещается по вертикали, то mg+ R =0, или mg =- R, или mg=N, т.е. сила трения в этом примере по величине равна
F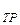 =
= mg.
mg.
Теперь силу F направим под углом  к горизонту (рис. 2.6,6). Векторная запись второго закона Ньютона аналогична предыдущему примеру. В проекциях на оси OX и OY этот закон запишется
к горизонту (рис. 2.6,6). Векторная запись второго закона Ньютона аналогична предыдущему примеру. В проекциях на оси OX и OY этот закон запишется
F cos — F
— F = ma и mg—R—F sin
= ma и mg—R—F sin =0.
=0.
Последнее соотношение позволяет определить силу трения
F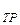 =
= 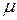 N =
N =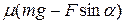
Таким образом, сила трения скольжения существенно зависит от направления приложенной силы F.
Пример 6. Определим силу трения скольжения при движении тела вдоль наклонной плоскости. В этом случае на тело действуют три силы: сила тяжести mg, реакция опоры R и сила трения F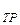 (рис. 6.7,а). И второй закон Ньютона записывается в виде
(рис. 6.7,а). И второй закон Ньютона записывается в виде
R + mg + F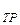 = ma
= ma
В проекциях на оси OX и OY выражение (2.18) можно записать уравнение движения в виде:
F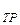 - mg sin
- mg sin = ma
= ma
R - mg cos =0
=0
Эти соотношения позволяют определить силу трения скольжения вдоль наклонной плоскости. Действительно,
R=N=mgcosa и F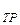 =
=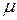 mg cos
mg cos
Если тело покоится на наклонной плоскости, то правая часть уравнения движения обращается в нуль. Однако при некоторых значениях угла наклона тело не сможет покоиться на наклонной плоскости и начнет двигаться.
Определим этот максимальный угол наклона 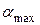 .С одной стороны, сила трения должна расти с ростом угла наклона, так как F
.С одной стороны, сила трения должна расти с ростом угла наклона, так как F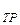 = mg sin
= mg sin но, с другой стороны, максимально возможная сила трения равна F
но, с другой стороны, максимально возможная сила трения равна F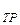 =
=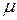 mg cos
mg cos . При
. При  =
=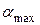 сила трения покоя достигает своего максимально возможного значения:
сила трения покоя достигает своего максимально возможного значения:
F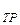 = F
= F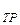
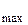 или mg sin
или mg sin
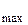 =
=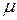 mg cos
mg cos .
.
Отсюда
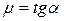
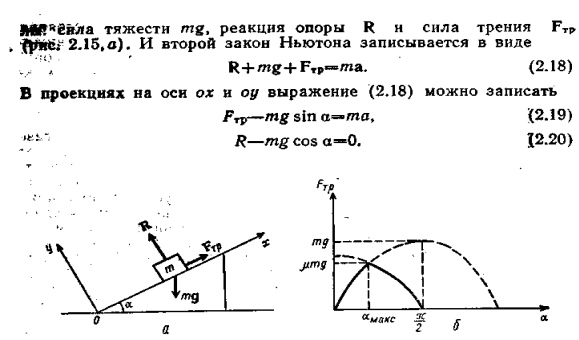 |
Рис.6.7.
Таким образом, когда тангенс угла наклона становится равным коэффициенту трения, тело начинает соскальзывать с наклонной плоскости. График зависимости силы трения от угла наклона приведен на рис.6.7,б.
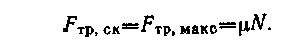 |
При скольжении сила трения зависит не только от состояния трущихся поверхностей, но и от относительной скорости движения тел. Однако при не слишком больших относительных скоростях движения сила трения скольжения мало отличается от максимального значения силы трения покоя, т. е.
ДИНАМИКА ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ
15. КИНЕТИЧЕСКАЯ ЭНЕРГИЯ ВРАЩАЮЩЕГОСЯ ТЕЛА. МОМЕНТ ИНЕРЦИИ.
До сих пор мы рассматривали движение таких тел, размерами и формой которых можно было пренебречь в данных условиях, т. е. движение материальных точек (частиц). Теперь перейдем к рассмотрению тел, имеющих конечные размеры. При этом будем рассматривать абсолютно твердое тело. Абсолютно твердым телом называется такое тело, в котором взаимное расположение отдельных частиц при движении не изменяется. Простейшими видами движения абсолютно твердого тела являются поступательное и вращение тела вокруг оси (вращательное движение). При поступательном движении твердого тела все его точки в любой момент времени имеют одинаковую скорость, описывают траектории одинаковой формы (смещенные относительно друг друга).
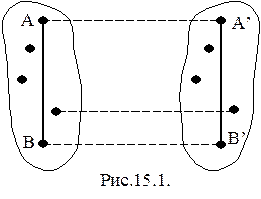 Любой отрезок прямой АВ (рис.15.1), соединяющий две точки тела, при поступательном движении остается параллельным самому себе (АВççА¢В¢). При вращении твердого тела вокруг оси (рис.15.2) все точки тела описывают окружности с центрами, лежащими на оси в плоскостях, перпендикулярных оси вращения.
Любой отрезок прямой АВ (рис.15.1), соединяющий две точки тела, при поступательном движении остается параллельным самому себе (АВççА¢В¢). При вращении твердого тела вокруг оси (рис.15.2) все точки тела описывают окружности с центрами, лежащими на оси в плоскостях, перпендикулярных оси вращения.

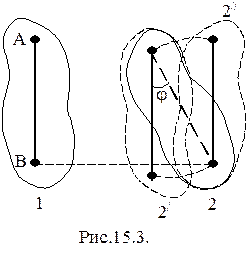
Линейные скорости точек, очевидно, зависят от их расстояния до оси вращения, а угловые их скорости одинаковы.
Любое движение твердого тела может быть сведено к простейшим - поступательному и вращательному. Пусть тело при своем движении переместится из положения 1 в положение 2 (рис. 15.3).
Это перемещение можно представить следующим образом: сначала тело перемещается поступательно, так, чтобы какая - либо точка (А в положении 2¢ или В в положении 2¢¢) попала в свое обычное положение, а затем путем вращения вокруг этой точки на угол j, тело перейдет в конечное положение. Таким образом, произвольное движение твердого тела можно представить себе в виде совокупности поступательного движения произвольной точки тела и вращения тела вокруг оси, проходящей через эту точку.
КИНЕТИЧЕСКАЯ ЭНЕРГИЯ ВРАЩАЮЩЕГОСЯ ТЕЛА.
При поступательном движении твердого тела все его точки в любой момент времени движутся с одинаковой скоростью  . Поэтому кинетическая энергия поступательно движущегося тела массой М равна
. Поэтому кинетическая энергия поступательно движущегося тела массой М равна
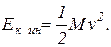 (15.1)
(15.1)
При вращательном движении твердого тела его можно представить как совокупность элементарных частиц, масса которых m1, m2,..., mn, которые находятся на расстояниях от оси вращения r1, r2,..., rn и движутся со скоростями  . Кинетическая энергия вращающегося тела Екин равна сумме кинетических энергий материальных точек, из которых твердое тело состоит:
. Кинетическая энергия вращающегося тела Екин равна сумме кинетических энергий материальных точек, из которых твердое тело состоит:
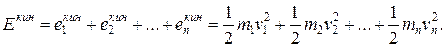 (15.2)
(15.2)
Но vn = w rn, где w - угловая скорость вращения тела. Учитывая это, запишем:
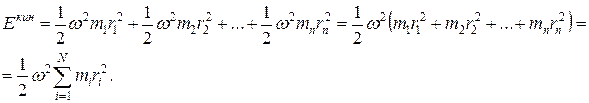
Мы видим, что кинетическая энергия вращающегося тела зависит от его размеров и расположения частиц различной массы (распределения масс) относительно оси вращения. Величина
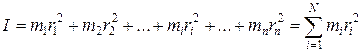 (15.3)
(15.3)
характеризует, как мы увидим дальше, инертность вращающегося тела. Она называется моментом инерции тела относительно данной оси вращения. Введя величину момента инерции I, запишем окончательно для кинетической энергии вращающегося тела
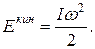 (15.4)
(15.4)
В том случае, когда тело участвует одновременно в поступательном и вращательном движении, его кинетическая энергия будет
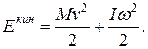 (15.5)
(15.5)
Частным случаем такого движения может служить тело круглого сечения (обруч, диск, шар, цилиндр), катящееся без скольжения по плоскости.
В качестве примера вычислим момент инерции однородного сплошного цилиндра высотой h и радиусом R относительно его геометрической оси.
ЗНАЧЕНИЯ МОМЕНТОВ ИНЕРЦИИ НЕКОТОРЫХ ТЕЛ
16. ТЕОРЕМА ШТЕЙНЕРА.
Как уже было показано выше, момент инерции тела равен сумме моментов инерции составляющих это тело частиц.
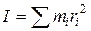 . (16.1)
. (16.1)
Чем мельче размеры этих частиц, тем точнее вычисляется сумма. При переходе к бесконечно малому размеру частиц сумма превращается в интеграл:
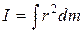 . (16.2)
. (16.2)
Точно вычислить этот интеграл удается только для тел простой формы, например, для тел вращения (шара, диска, цилиндра) относительно осей, проходящих через их центр масс.
В случаях, когда необходимо вычислить момент инерции относительно некоторой оси, не проходящей через центр масс, пользуются теоремой Штейнера:
Момент инерции I относительно произвольной оси равен сумме момента инерции Iс относительно оси, параллельно данной и проходящей через центр масс тела, и произведения массы тела m на квадрат расстояния l между осями (рис.16.1):
I = Ic + ml2. (16.3)
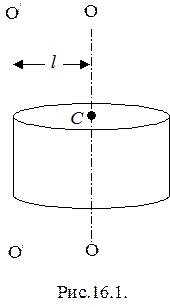
Таким образом, если известен момент инерции относительно оси OO (рис.16.1), проходящей через центр масс С и масса тела, то пользуясь теоремой Штейнера можно вычислить момент инерции относительно произвольной оси O¢O¢ расположенной параллельно OO на расстоянии l.
17. ОСНОВНОЙ ЗАКОН ДИНАМИКИ ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ
Рассмотрим вращение твердого тела (рис.17.1) вокруг некоторой оси РР¢ под влиянием сил, действующих на него. Разобьем тело на N материальных точек. Масса i- й точки mi. На каждую i- ю точку действуют силы взаимодействия с другими точками, а также внешняя сила. При разложении сил, действующих на любую точку тела, следует учитывать только составляющие сил, лежащие в плоскостях, перпендикулярных оси вращения РР¢, так как составляющие, параллельные оси вращения, могут вызвать только смещение тела вдоль оси, а не его вращение. Итак, если на i- ю точку, находящуюся на расстоянии 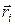 от оси вращения, действует внешняя сила
от оси вращения, действует внешняя сила 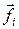 и сила взаимодействия этой точки с k-й точкой
и сила взаимодействия этой точки с k-й точкой 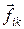 , то по второму закону Ньютона имеем
, то по второму закону Ньютона имеем
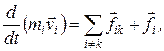 (17.1)
(17.1)
где 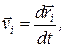 индекс k принимает все значения от 1 до N, кроме i (точка не взаимодействует сама с собой).
индекс k принимает все значения от 1 до N, кроме i (точка не взаимодействует сама с собой).

Ранее мы видели, что инерционные свойства твердого тела при вращении зависят от распределения массы тела относительно оси вращения (от расстояния каждой точки от оси вращения). Поэтому преобразуем записанное нами равенство. Умножим векторно обе части равенства на 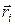 :
:
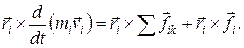 (17.2)
(17.2)
В левой части равенства знак производной 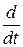 можно вынести за знак векторного произведения, так как:
можно вынести за знак векторного произведения, так как:
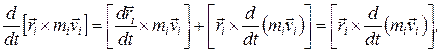 (17.3)
(17.3)
потому что
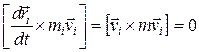 (17.4)
(17.4)
(векторы  и
и  направлены одинаково, а для таких векторов векторное произведение равно нулю).
направлены одинаково, а для таких векторов векторное произведение равно нулю).
Таким образом, наше уравнение будет иметь вид
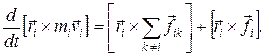 (17.5)
(17.5)
Векторное произведение радиус-вектора  , проведенного в точку приложения силы
, проведенного в точку приложения силы 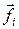 , и этой силы называется моментом
, и этой силы называется моментом 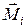 силы
силы 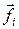 относительно точки O (рис.17.2). Численное значение момента силы Мi равно
относительно точки O (рис.17.2). Численное значение момента силы Мi равно
Mi = firi sin ai = fi li , (17.6)
где ai - угол между векторами 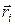 и
и 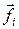 , а li = ri sin ai - длина перпендикуляра, опущенного из точки O на линию действия силы
, а li = ri sin ai - длина перпендикуляра, опущенного из точки O на линию действия силы 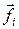 , т. е. кратчайшее расстояние от направления силы, действующей на i -ю точку, до центра вращения этой точки.
, т. е. кратчайшее расстояние от направления силы, действующей на i -ю точку, до центра вращения этой точки.
Момент силы 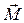 характеризует способность силы изменять скорость вращения тела относительно некоторой оси (точки). Причем это действие будет тем эффективнее, чем больше плечо поворачивающей силы l = r sina. Если же сила приложена так, что ее плечо равно нулю (r=0 или sin a=0), то, какой бы большой не была сила, скорость вращения не изменится.
характеризует способность силы изменять скорость вращения тела относительно некоторой оси (точки). Причем это действие будет тем эффективнее, чем больше плечо поворачивающей силы l = r sina. Если же сила приложена так, что ее плечо равно нулю (r=0 или sin a=0), то, какой бы большой не была сила, скорость вращения не изменится.
Если теперь просуммировать уравнение, полученное для одной точки, по всем N точкам твердого тела, то получим:
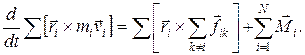 (17.7)
(17.7)
Векторная сумма  моментов всех внешних сил, действующих на точки тела, называется главным моментом
моментов всех внешних сил, действующих на точки тела, называется главным моментом 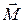 внешних сил относительно оси РР¢.
внешних сил относительно оси РР¢.
Векторное произведение радиус-вектора 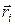 i- й точки тела на вектор количества движения
i- й точки тела на вектор количества движения 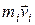 этой точки называется моментом импульса этой точки
этой точки называется моментом импульса этой точки 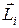 :
:
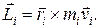 (17.8)
(17.8)
Векторная сумма моментов импульса всех материальных точек тела называется моментом импульса тела относительно оси РР¢:
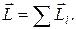 (17.9)
(17.9)
И, наконец, векторная сумма моментов всех внутренних сил относительно той же оси РР¢ равна нулю:
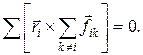 (17.10)
(17.10)
так как в соответствии с третьим законом Ньютона 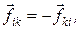 а линии действия этих сил - общие.
а линии действия этих сил - общие.
С учетом всех этих выводов получим окончательно:
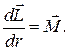 (17.11)
(17.11)
Скорость изменения момента импульса твердого тела, вращающегося вокруг неподвижной оси, равна главному моменту всех внешних сил, приложенных к телу. Это и есть основной закон динамики для вращательного движения твердого тела.
Рассмотрим подробнее величину момента импульса тела:
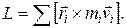 (17.11)
(17.11)
Учитывая, что 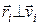 (радиус окружности и касательная к ней), можно записать, что численное значение Li будет:
(радиус окружности и касательная к ней), можно записать, что численное значение Li будет:
Li = ri mi vi (17.12)
Если заменить vi =ri w, то получим: 
Li = mi ri2w (17.13)
Для твердого тела получим
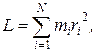 (17.14)
(17.14)
но
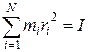 (17.15)
(17.15)
есть момент инерции тела относительно оси вращения РР¢, поэтому запишем
L = I w. (17.16)
Сравнив выражения
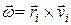 и
и 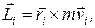 (17.17)
(17.17)
увидим, что вектор количества движения 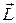 для всех точек тела и вектор угловой скорости тела
для всех точек тела и вектор угловой скорости тела  направлены одинаково, поэтому можно записать
направлены одинаково, поэтому можно записать
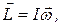 (17.18)
(17.18)
где 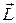 - момент импульса тела;
- момент импульса тела;  - его угловая скорость; I - момент инерции тела.
- его угловая скорость; I - момент инерции тела.
С учетом всего изложенного выше запишем основной закон динамики вращательного движения тела в виде:
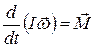 или
или 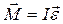 . (17.19)
. (17.19)
Основной закон динамики вращательного движения является аналогом второго закона Ньютона для поступательного движения. Причиной, определяющей характер вращательного движения, выступает аналог силы - момент силы. Мерой инертности тела при вращательном движении выступает аналог массы - момент инерции, который учитывает каким образом масса тела расположена относительно оси вращения. Результатом воздействия момента силы на тело является изменение скорости его вращения, т. е. угловое ускорение - аналог линейного ускорения.
18. ЗАКОН СОХРАНЕНИЯ МОМЕНТА ИМПУЛЬСА.
Рассмотрим теперь произвольную систему материальных точек (не обязательно твердое тело). Если на каждую точку системы действуют внешняя сила и силы взаимодействия этой точки с другими точками системы, то по второму закону Ньютона имеем
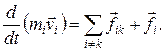 (18.1)
(18.1)
Умножив векторно обе части равенства на 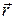 и проведя все преобразования, которые мы проводили для твердого тела, получим:
и проведя все преобразования, которые мы проводили для твердого тела, получим:
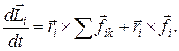 (18.2)
(18.2)
Также как и в случае твердого тела имеем
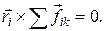 (18.3)
(18.3)
и поэтому
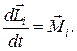 (18.4)
(18.4)
где 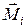 - момент внешних сил, действующих на i -ю точку:
- момент внешних сил, действующих на i -ю точку:
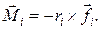 (18.5)
(18.5)
Просуммировав по всем точкам системы, получим
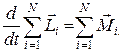 (18.6)
(18.6)
Если векторная сумма 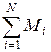 всех внешних сил, действующих на систему, равна нулю, то
всех внешних сил, действующих на систему, равна нулю, то
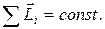 (18.7)
(18.7)
Мы пришли к выводу еще одного закона сохранения - закона сохранения момента импульса изолированной (замкнутой) системы тел. Момент импульса изолированной системы тел не изменяется со временем. Это нужно понимать так: в изолированной системе тел моменты импульса отдельных тел могут со временем изменяться, но при этом векторная сумма моментов импульса всех тел системы остается неизменной, т. е. внутренние взаимодействия не могут изменить суммарный момент импульса изолированной системы.
|
|
|
|
|
Дата добавления: 2014-01-11; Просмотров: 3050; Нарушение авторских прав?; Мы поможем в написании вашей работы!