
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Элементы специальной теории относительности
|
|
|
|
13. ПРЕОБРАЗОВАНИЯ ГАЛИЛЕЯ. МЕХАНИЧЕСКИЙ ПРИНЦИП ОТНОСИТЕЛЬНОСТИ
В классической механике справедлив механический принцип относительности (принцип относительности Галилея): законы динамики одинаковы во всех инерциальных системах отсчета.
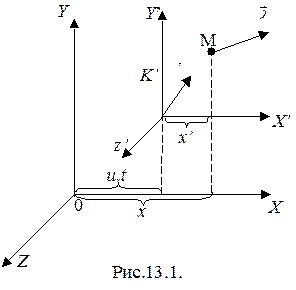
Для его доказательства сначала получим формулы преобразования координат, которые в классической механике носят название преобразования координат Галилея.
Рассмотрим две инерциальные системы координат К и К¢ (рис.13.1). Условно примем систему координат К неподвижной. Тогда система координат К¢ движется относительно системы К со скоростью u (переносная скорость). Для упрощения математических записей будем считать, что в начальный момент времени (t = 0) обе системы координат совпадали. Тогда в некоторый момент времени t координаты точки М в системе К будут x, y, z, а в системе К¢ - x¢, y¢, z¢. Из чертежа видно, что между координатами x и x¢ существует такая зависимость:
х = х¢ + uхt, (13.1)
где uх - составляющая переносной скорости u по оси х. Аналогично для двух других координат можно получить:
y = y¢ + uyt, (13.2)
z = z¢ + uzt. (13.3)
В этих формулах подразумевается, что ход времени во всех инерциальных системах отсчета одинаков (t = t¢), т. е. ход времени не зависит от того, движутся точки или неподвижны. Это является постулатом в классической механике.
Если точка М движется в пространстве, то очевидно, что скорости ее относительно системы К - v и относительно системы К¢ - v ¢ не одинаковы. Составляющие этих скоростей по осям координат могут быть найдены так:
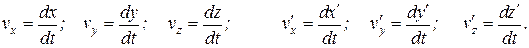 (13.4)
(13.4)
Взяв производные от правых и левых частей формул преобразования координат (13.1) - (13.3), получим:
vx = v¢х + uх; vу = v¢y + uy; v¢z = v¢z + uz. (13.5)
По правилу сложения векторов имеем:
 (13.6)
(13.6)
и тогда окончательно получим
 (13.7)
(13.7)
Это векторное равенство выражает правило сложения скоростей в классической механике.
И, наконец, рассмотрим точку, движущуюся в пространстве неравномерно (с ускорением). Ускорение точки в системах координат К и К¢ можно представить в виде суммы компонент:
 ; (13.8)
; (13.8)
 .
.
По определению
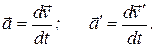 (13.9)
(13.9)
Взяв производную по времени от правой и левой частей равенства (13.7), выражающего правило сложения скоростей, принимая во внимание, что переносная скорость u постоянна во времени, получим:
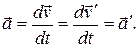 (13.10)
(13.10)
Ускорение точки в различных инерциальных системах отсчета одинаково. Это уравнение подтверждает механический принцип относительности: уравнения динамики при переходе от одной инерциальной системы отсчета к другой не изменяются.
Пример 1. Два поезда движутся навстречу друг другу. Величины их скоростей соответственно равны: 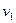 =60 км/ч и
=60 км/ч и 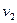 =90 км/ч (рис. 13.2,а). Определим скорость первого поезда относительно второго и второго относительно первого.
=90 км/ч (рис. 13.2,а). Определим скорость первого поезда относительно второго и второго относительно первого.
Свяжем неподвижную систему координат 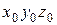 , например с Землей, а подвижную xyz — со вторым поездом, движущимся со скоростью
, например с Землей, а подвижную xyz — со вторым поездом, движущимся со скоростью 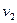 (рис- 13.2,б). Тогда движение второго поезда относительно Земли будет переносным. Движение первого поезда относительно Земли (неподвижной системы
(рис- 13.2,б). Тогда движение второго поезда относительно Земли будет переносным. Движение первого поезда относительно Земли (неподвижной системы 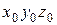 ) — абсолютным. Скорость первого поезда относительно второго поезда (относительно подвижной системы xyz) является относительной. Следовательно, при таком выборе системы координат
) — абсолютным. Скорость первого поезда относительно второго поезда (относительно подвижной системы xyz) является относительной. Следовательно, при таком выборе системы координат 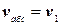 ,
, 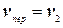 ,
, 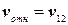 , закон сложения скоростей
, закон сложения скоростей  запишется:
запишется:  . Отсюда относительная скорость равна
. Отсюда относительная скорость равна 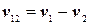 Выполним вычитание векторов (см. рис. 13.2,в). Из рисунка видно, что в проекциях на ось ОХ последнее уравнение имеет вид:
Выполним вычитание векторов (см. рис. 13.2,в). Из рисунка видно, что в проекциях на ось ОХ последнее уравнение имеет вид: 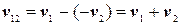 .Скорость первого поезда относительно второго равна сумме модулей скоростей
.Скорость первого поезда относительно второго равна сумме модулей скоростей  и
и  и направлено в сторону оси ОХ.
и направлено в сторону оси ОХ.
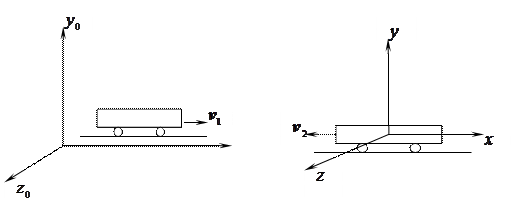 |

Рис. 12.2. Относительное движение двух тел, движущихся навстречу друг другу
(объяснение см. в тексте)
Чтобы определить скорость второго поезда относительно первого, удобно подвижную систему координат XOY связать с первым поездом, а неподвижную систему координат 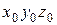 по-прежнему оставить связанной с Землей. Тогда
по-прежнему оставить связанной с Землей. Тогда  ,
, 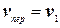 ,
, 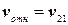 . При таком выборе систем координат закон сложения скоростей запишется
. При таком выборе систем координат закон сложения скоростей запишется
 или
или 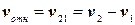 .
.
Векторное вычитание скоростей изображено на рис.1.42, г.
В проекции на ось ОХ значение относительной скорости  равно
равно
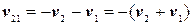 .
.
Как видно, скорость второго поезда относительно первого равна сумме скоростей  и
и  , но направлена в сторону, противоположную оси OX.
, но направлена в сторону, противоположную оси OX.
Пример 2. По пересекающимся под углом  шоссейным дорогам движутся две автомашины со скоростями
шоссейным дорогам движутся две автомашины со скоростями  и
и  (рис. 13.3,а). Определить величину и направление скорости первого автомобиля относительно второго.
(рис. 13.3,а). Определить величину и направление скорости первого автомобиля относительно второго.

Рис.13.3. Относительное движение двух тел, движущихся под углом  .
.
Неподвижную систему координат 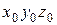 свяжем с Землей. Подвижную - xyz — с автомашиной, движущейся со скоростью
свяжем с Землей. Подвижную - xyz — с автомашиной, движущейся со скоростью 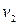 . Тогда движение этой автомашины будет переносным. В системе координат xyz движение первой автомашины будет относительным, а ее движение относительно Земли — абсолютным, т. е.
. Тогда движение этой автомашины будет переносным. В системе координат xyz движение первой автомашины будет относительным, а ее движение относительно Земли — абсолютным, т. е.
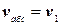 ,
, 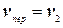 ,
, 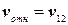 ,
,
Пользуясь законом сложения скоростей, запишем
 или
или 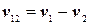 .
.
Вычитание векторов показано на рис.1.43,б. Вектор  является скоростью первой автомашины относительно второй. Модуль этой скорости определяется по теореме косинусов
является скоростью первой автомашины относительно второй. Модуль этой скорости определяется по теореме косинусов
 .
.
Пример 3. Разгоняясь, поезд проходит первую часть своего пути с ускорением 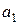 , за время
, за время 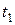 . Далее он идет равномерно и проходит вторую часть пути за время
. Далее он идет равномерно и проходит вторую часть пути за время  , затем поезд тормозит с постоянным ускорением до полной остановки и тратит на это время
, затем поезд тормозит с постоянным ускорением до полной остановки и тратит на это время  . Определить путь, пройденный поездом, и его среднюю скорость на этом пути.
. Определить путь, пройденный поездом, и его среднюю скорость на этом пути.
Поезд движется в течении времени (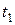 +
+ +
+ ). В интервале
). В интервале 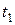 движение прямолинейное равноускоренное с нулевой начальной скоростью. Следовательно, скорость и путь в любой момент времени определяются формулами:
движение прямолинейное равноускоренное с нулевой начальной скоростью. Следовательно, скорость и путь в любой момент времени определяются формулами:
 ,
, 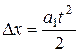
При t =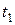 поезд достигает скорости
поезд достигает скорости  и начинается равномерное движение с постоянной скоростью
и начинается равномерное движение с постоянной скоростью 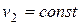 в течении времени
в течении времени  и проходит путь
и проходит путь 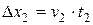 . При
. При 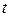 =
=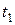 +
+ начинается равнозамедленное движение с начальной скоростью, равной
начинается равнозамедленное движение с начальной скоростью, равной  . Скорость
. Скорость  и пройденный путь
и пройденный путь  определяются выражениями:
определяются выражениями:
 ;
; 
Из выражения для скорости можно определить неизвестное в задаче ускорение 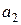 , с которым поезд тормозит на третьем участке пути. Поскольку поезд тормозит до полной остановки, то
, с которым поезд тормозит на третьем участке пути. Поскольку поезд тормозит до полной остановки, то  =0. Следовательно,
=0. Следовательно,  .
.
Так как поезд не меняет направления движения, то путь, пройденный им, равен сумме перемещений 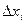 , т. е.
, т. е.
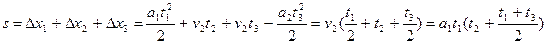
Средняя скорость на всем пути равна сумме всех перемещений, деленной на полное время движения тела, т.е.

Пример 4. Тело начинает двигаться из точки А со скоростью  и через некоторое время попадает в точку В (рис. 13.4). Какой путь прошло тело, если оно двигалось с постоянным ускорением а? Расстояние между точками А и В равно l. Определить среднюю скорость тела за время движения от точки А до точки В.
и через некоторое время попадает в точку В (рис. 13.4). Какой путь прошло тело, если оно двигалось с постоянным ускорением а? Расстояние между точками А и В равно l. Определить среднюю скорость тела за время движения от точки А до точки В.
Расположим ось OX вдоль направления скорости v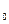 , поместив начало координат в точку А. Так как тело попадает в точку В с координатой х = - l, то его ускорение направлено противоположно скорости v
, поместив начало координат в точку А. Так как тело попадает в точку В с координатой х = - l, то его ускорение направлено противоположно скорости v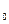 . В этом случае для любого момента времени уравнение для координаты будет иметь вид:
. В этом случае для любого момента времени уравнение для координаты будет иметь вид:

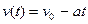
В некоторой точке С скорость тела обращается в нуль, и тело меняет направление движения. Это соответствует моменту времени  . В этот момент времени тело будет находиться на максимальном расстоянии от точки А, равном:
. В этот момент времени тело будет находиться на максимальном расстоянии от точки А, равном:
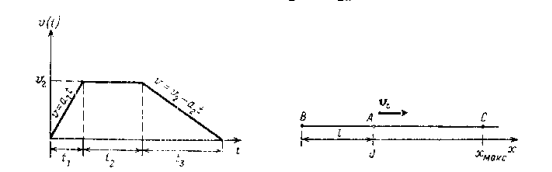 |
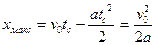
Рис.13.4. График зависимости скорости от времени | Рис.13.5 |
Путь, пройденный телом при движении от точки А до точки В, равен: s = 2AC+AB = 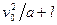 . Время полного движения
. Время полного движения 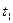 определяется из уравнения для координаты:
определяется из уравнения для координаты:

В нашей задаче в выражении 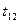 перед корнем следует ставить «+», так как отрицательное значение полного времени движения не имеет физического смысла. Средняя скорость движения тела на всем пути равна:
перед корнем следует ставить «+», так как отрицательное значение полного времени движения не имеет физического смысла. Средняя скорость движения тела на всем пути равна:
14. ЭЛЕМЕНТЫ СПЕЦИАЛЬНОЙ ТЕОРИИ ОТНОСИТЕЛЬНОСТИ.
Законы движения макроскопических тел со скоростями, сравнимыми со скоростью света с (релятивистских частиц), изучаютсярелятивистской механикой, основанной на специальной теории относительности, сформулированной А. Эйнштейном. Основу этой теории образуют два постулата:
1. Принцип относительности Эйнштейна, который является распространением механического принципа относительности галилея на все без исключения физические явления: “все законы природы инвариантны по отношению к переходу от одной инерциальной системы остчета к другой”.
2. Принцип постоянства скорости света: “скорость света в вакууме одинакова во всех инерциальных системах отсчета и не зависит от скорости движения источника света или наблюдателя”.
Из этих постулатов вытекают важные выводы относительно свойств пространства и времени.
Преобразования координат и скоростей Галилея противоречат принципу постоянства скорости света. В специальной теории относительности они заменены на преобразования Лоренца:
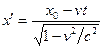

 (14.1)
(14.1)
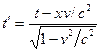
где x, y, z – координаты в неподвижной системе координат, x1, y1, z1 – координаты в системе, движущейся относительно первой со скоростью v.
Некоторые следствия специальной теории относительности.
1. Длина тел в разных системах отсчета.
l=l0√1-v2/c2 (14.2)
Длина стержня l, измеренная в системе координат, относительно которой он движется, меньше длины l0 в системе координат, относительно которой он покоится. Т.е. у движущихся тел размеры их в направлении движения сокращаются тем больше, чем больше скорость движения. Это явление называется лоренцевым сокращением.
2. Длительность событий в разных системах координат.
∆t=∆t0/(√1-v2/c2) (14.3)
Длительность события, происходящего в некоторой точке, наименьшая в той инерциальной системе координат, относительно которой эта точка неподвижна.
Или: часы, движущиеся относительно инерциальной системы отсчета, идут медленнее покоящихся часов.
3. Основной закон релятивистской динамики материальной точки.
Масса движущихся релятивистских частиц зависит от их скорости:
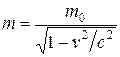 , (14.4)
, (14.4)
где т 0 — масса покоя частицы, т. е. масса, измеренная в той инерциальной системе отсчета, относительно которой частица находится в покое; с — скорость света в вакууме; т — масса частицы в системе отсчета, относительно которой она движется со скоростью v. Следовательно, масса одной и той же частицы различна в разных инициальных системах отсчета.
Из принципа относительности, утверждающего инвариантность всех законов природы при переходе от одной инерциальной системы отсчета к другой, следует условие инвариантности уравнений физических законов относительно преобразований Лоренца. Основной закон динамики Ньютона
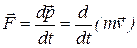 (14.5)
(14.5)
оказывается также инвариантным по отношению к преобразованиям Лоренца, если в нем справа стоит производная по времени от релятивистского импульса. Основной закон релятивистской динамики материальной точки имеет вид
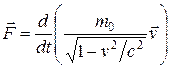 (14.6)
(14.6)
или
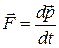 , (14.7)
, (14.7)
где
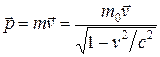 (14.8)
(14.8)
— релятивистский импульс материальной точки.
Отметим, что основной закон релятивистской динамики внешне совпадает с основным уравнением ньютоновской механики. Однако физический смысл его другой: справа стоит производная по времени от релятивистского импульса. Таким образом, данное уравнение инвариантно по отношению к преобразованиям Лоренца и, следовательно, удовлетворяет принципу относительности Эйнштейна. Следует учитывать, что ни импульс, ни сила не являются инвариантными величинами. Более того, в общем случае ускорение не совпадает по направлению с силой.
В силу однородности пространства в релятивистской механике выполняетсязакон сохранения релятивистского импульса: релятивистский импульс замкнутой системы сохраняется, т. е. не изменяется с течением времени.
Законы классической механики получаются как следствие теории относительности для предельного случая v<<c. Таким образом, классическая механика — это механика макротел, движущихся с малыми скоростями (по сравнению со скоростью света в вакууме).
Экспериментальное доказательство зависимости массы от скорости является подтверждением справедливости специальной теории относительности.
4. Закон взаимосвязи массы и энергии
Полная энергия Е релятивистской частицы с массой т:
 . (14.9)
. (14.9)
Таким образом, полная энергия системы равна произведению ее массы на квадрат скорости света в вакууме. Это есть закон взаимосвязи (пропорциональности) массы и энергии, имеющий универсальный характер. Он применим ковсем формам энергии, т.е. можно утверждать, что с энергией, какой бы формы она ни была, связана масса
m=E/c2 (14.10)
и, наоборот, со всякой массой связана энергия. Отметим, что в полную энергию Е не входит потенциальная энергия тела во внешнем силовом поле.
Из уравнения (14.9) следует, что при v=0 (когда тело покоится), оно обладает энергией
E0 = m o c 2, (14.11)
называемой энергией покоя.В классической механике энергия покоя E 0 не учитывается, считая, что при v= 0 энергия покоящегося тела равна нулю.
.
РАБОТА И ЭНЕРГИЯ
9. КИНЕТИЧЕСКАЯ ЭНЕРГИЯ, РАБОТА, МОЩНОСТЬ, КПД.
Энергия — универсальная мера различных форм движения и взаимодействия. С различными формами движения материи связывают различные формы энергии: механическую, тепловую, электромагнитную, ядерную и др.
Существует два вида механической энергии: кинетическая и потенциальная.
Кинетическая энергия механической системы — это энергия механического движения этой системы.
Запишем уравнение второго закона Ньютона для частицы с постоянной массой m, на которую действует некоторая равнодействующая сил
 (9.1)
(9.1)
Умножим это равенство на равенство, определяющее элементарный путь dS, пройденный частицей при ее движении под действием силы F:
dS = vdt. (9.2)
В результате умножения получим следующее равенство:
FdS = mvdv. (9.3)
Но произведение mvdv можно представить в виде:
 (9.4)
(9.4)
и поэтому можно записать:
 (9.5)
(9.5)
Величина, стоящая под знаком дифференциала в правой части равенства, есть кинетическая энергия Екин материальной точки
 (9.6)
(9.6)
Таким образом, тело массы m, движущееся со скоростью v, обладает кинетической энергией E = 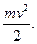 Из формулы видно, что кинетическая энергия зависит только от массы и скорости тела, т.е. кинетическая энергия системы есть функция состояния ее движения.
Из формулы видно, что кинетическая энергия зависит только от массы и скорости тела, т.е. кинетическая энергия системы есть функция состояния ее движения.
Величина, стоящая в левой части равенства (9.3), есть элементарная работа силы F на пути dS: dA = FdS.
Понятиеработы силы вводится, чтобы количественно характеризовать процесс обмена энергией между взаимодействующими телами. В общем виде элементарная работа силы dA выражается как скалярное произведение:
 (9.7)
(9.7)
где a - угол между направлением силы  и направлением перемещения
и направлением перемещения  .
.
Из формулы (9.7) видно, что при изменении угла  между приложенной силой F и перемещением
между приложенной силой F и перемещением 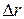 от 0 до
от 0 до  работа положительна (
работа положительна ( >0), при угле
>0), при угле  , меняющемся от
, меняющемся от  до
до , работа отрицательна (
, работа отрицательна ( <0). При значении
<0). При значении  =
= работа
работа  =0, т. е. если сила перпендикулярна перемещению, то она работу не совершает. Следует отметить, что работа не совершается, если точка приложения силы не перемещается в выбранной системе отсчета, т. е. если |
=0, т. е. если сила перпендикулярна перемещению, то она работу не совершает. Следует отметить, что работа не совершается, если точка приложения силы не перемещается в выбранной системе отсчета, т. е. если | 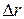 |=0.
|=0.
Работа силы на участке траектории от точки 1 до точки 2 равна алгебраической сумме элементарных работ на отдельных бесконечно малых участках пути. Эта сумма приводится к интегралу
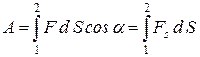 , (9.8)
, (9.8)
где 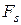 — проекция вектора
— проекция вектора  на вектор
на вектор  .
.
Единица энергии и работы —джоуль (Дж): 1 Дж — работа, совершаемая силой 1 Н на пути 1 м (1 Дж = 1 Н·м).
Чтобы охарактеризовать скорость совершения работы, вводят понятиемощности:
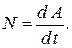 (9.9)
(9.9)
За время 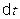 сила
сила  совершает работу
совершает работу 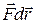 , и мощность, развиваемая этой силой, в данный момент времени
, и мощность, развиваемая этой силой, в данный момент времени
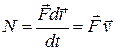 , (9.10)
, (9.10)
т. е. равна скалярному произведению вектора силы на вектор скорости, с которой движется точка приложения этой силы;  — величина скалярная.
— величина скалярная.
Единица мощности —ватт (Вт): 1 Вт — мощность, при которой за время 1 с совершается работа 1 Дж (1 Вт=1 Дж/с).
Если проинтегрировать соотношение
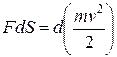 (9.11)
(9.11)
вдоль некоторой траектории от точки 1 до точки 2
 (9.12)
(9.12)
то в левой части равенства получим работу силы F на пути 1-2:
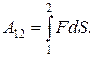 (9.13)
(9.13)
Правая часть равенства даст приращение кинетической энергии частицы при перемещении ее из точки 1 в точку 2:
 (9.14)
(9.14)
Полученные результаты можно сформулировать так: работа равнодействующих всех сил, действующих на частицу, идет на приращение ее кинетической энергии.
Каждая машина приводится в движение двигателем и предназначается для определенной работы. Но двигатель, приводящий машину в действие, выполняет кроме полезной работы, для которой предназначена машина, еще и дополнительную, но неизбежную работу, например работу против силы трения. Поэтому двигатели всегда выполняют большую работу, чем приводимая ими в действие машина.
Если работу, совершаемую машиной, обозначить 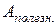 , а двигателем —
, а двигателем —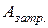 , то можно ввести величину, характеризующую экономичность машины. Эта величина, называемая коэффициентом полезного действия (КПД) обозначаемая греческой буквой
, то можно ввести величину, характеризующую экономичность машины. Эта величина, называемая коэффициентом полезного действия (КПД) обозначаемая греческой буквой 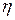 , равна
, равна
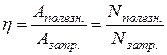 (9.15)
(9.15)
Ясно, что коэффициент полезного действия всегда меньше единицы. Чем ближе 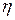 к единице, тем экономичнее, лучше машина. Коэффициент полезного действия часто выражают в процентах:
к единице, тем экономичнее, лучше машина. Коэффициент полезного действия часто выражают в процентах:
 (9.16)
(9.16)
Пример. Автомобиль массой т =1 т, трогаясь с места и двигаясь равноускоренно, проходит путь s=20 м за время  =2с. Какая минимальная мощность должна быть у двигателя этого автомобиля?
=2с. Какая минимальная мощность должна быть у двигателя этого автомобиля?
Для тела, движущегося с ускорением, значения средней мощности ( ) и мгновенной мощности (
) и мгновенной мощности ( ) не совпадают, так как не совпадают значения средней и мгновенной скоростей (рис. 3.11). Мгновенная мощность двигателя автомобиля и средняя мощность равны соответственно
) не совпадают, так как не совпадают значения средней и мгновенной скоростей (рис. 3.11). Мгновенная мощность двигателя автомобиля и средняя мощность равны соответственно
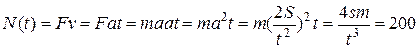 кВт,
кВт,
 кВт
кВт
Если автомобиль не сможет развить мощность N(t), то он не сможет развить и среднюю мощность Ncp, поскольку среднее значение скорости зависит от конечного значения мгновенной скорости v(t) (см. рис. 3.11). Поэтому значение мгновенной мощности, развиваемой двигателем автомобиля, в некоторый момент  будет необходимой минимальной мощностью.
будет необходимой минимальной мощностью.
10. ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ.
Потенциальная энергия — механическая энергия системы тел, определяемая их взаимным расположением и характером сил взаимодействия между ними.
Любое взаимодействие тел осуществляется через посредство материальной среды, которая называется полем. Если известна величина и направление силы (вектор силы), действующей на частицу в каждой точке пространства, то это значит, что частица находится в силовом поле. В этом случае для описания состояния частицы и изменения его не обязательно рассматривать тела, взаимодействие с которыми определяет состояние частицы. Простейшим из полей является стационарное поле, в котором силы поля, действующие на частицу в любой точке, не изменяются со временем.
Состояние частицы в классической механике полностью определяется ее положением в пространстве и вектором ее скорости или количеством движения. При переходе частицы из одной точки поля в другую ее состояние изменяется, а так как переход происходит под действием сил поля, то поле совершает работу, которая является количественной мерой изменения энергии взаимодействия частицы и поля.
Некоторые поля обладают очень важным свойством: если в таком поле частица движется по замкнутому пути, так что в результате движения она возвращается в исходное положение (в начальное состояние), то работа, совершаемая при этом силами поля, будет равна нулю. Из этого свойства поля следует утверждение: работа сил поля при переносе частицы из одной точки постоянного поля в другую не зависит от пути, по которому происходит перенос, а определяется только положением начальной и конечной точек пути (начальным и конечным состоянием частицы). Такое поле называется потенциальным полем, а действующие в нем силы называются консервативными.
Из этого утверждения нужно сделать вывод о том, что в каждой точке поля частица обладает энергией, которая зависит только от положения частицы в поле. Эта энергия называется потенциальной.
Примером такого поля могут служить гравитационное поле неподвижного тела и электрическое поле неподвижного электрического заряда.
Таким образом, работа сил поля А12 при переходе частицы из некоторой точки 1 в точку 2 равна разности потенциальных энергий Е1пот и Е2пот в соответствующих точках:
А12 = Е1пот = (Е2пот - Е1пот) = - dЕпот. (10.1)
Работа сил поля производится за счет убыли потенциальной энергии. Элементарная работа в потенциальном поле определяется
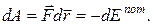 (10.2)
(10.2)
При переходе частицы между двумя бесконечно близкими точками разность  радиус-векторов конечной и начальной точек пути можно заменить отрезком пути
радиус-векторов конечной и начальной точек пути можно заменить отрезком пути  :
:
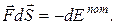 (10.3)
(10.3)
Учитывая, что
 , (10.4)
, (10.4)
где Fs - проекция вектора силы на направление перемещения, получим:
FSdS = - dЕпот, (10.5)
откуда
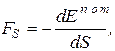 (10.6)
(10.6)
т. е. проекция силы на некоторое направление равна взятой с обратным знаком производной потенциальной энергии Епот по этому направлению. Знак “минус” в правой части равенства показывает, что проекция силы направлена в сторону убывания потенциальной энергии. Силы поля стремятся переместить частицу из точек с большей потенциальной энергией в точки с меньшим ее значением.
Конкретное выражение для потенциальной энергии зависит от характера силового поля. Например, потенциальная энергия тела массы m, поднятого на высоты h над поверхностью земли, равна
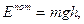 (10.7)
(10.7)
Потенциальная энергия является функцией состояния системы. Она зависит только от конфигурации системы и ее положения по отношению к внешним полям.
Полная энергия механической системы равна сумме кинетической и потенциальной энергий
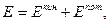 (10.8)
(10.8)
11. ЗАКОН СОХРАНЕНИЯ МЕХАНИЧЕСКОЙ ЭНЕРГИИ
Если в механической системе механическая энергия постепенно не преобразуется в другие (немеханические) формы энергии (например в тепло за счет работы силы трения), то полная механическая энергия системы сохраняется постоянной. Могут происходить лишь превращения кинетической энергии в потенциальную и обратно в эквивалентных количествах так, что полная энергия остается неизменной. В этом заключается закон сохранения механической энергии.
Закон сохранения и превращения энергии — фундаментальный закон природы, он справедлив как для систем макроскопических тел, так и для систем микротел.
Вставить стр. 25
Пример. Тележка массой М движется без трения по горизонтальным рельсам со скоростью  . На передний край тележки кладут тело массой т. Коэффициент трения между тележкой и телом
. На передний край тележки кладут тело массой т. Коэффициент трения между тележкой и телом 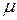 . Определить изменение кинетической энергии системы, состоящей из тележки и тела, если тело прошло относительно тележки расстояние l и остановилось (рис. 11.1).
. Определить изменение кинетической энергии системы, состоящей из тележки и тела, если тело прошло относительно тележки расстояние l и остановилось (рис. 11.1).
На тело в горизонтальном направлении действует только сила трения 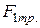 , которая увеличивает скорость тела относительно Земли. По третьему закону Ньютона на тележку в горизонтальном направлении действует сила трения
, которая увеличивает скорость тела относительно Земли. По третьему закону Ньютона на тележку в горизонтальном направлении действует сила трения  которая уменьшает скорость тележки.
которая уменьшает скорость тележки.
Тело перестанет скользить вдоль тележки тогда, когда их скорости относительно Земли станут одинаковыми. Сила трения в этом случае обратится в нуль, а тележка и тело будут двигаться как единое целое с некоторой постоянной скоростью относительно Земли и. К этому моменту времени тележка пройдет относительно Земли расстояние s, а тело — расстояние (s—l) (см. рис. 3.15).
Сила трения  совершает положительную работу:
совершает положительную работу:
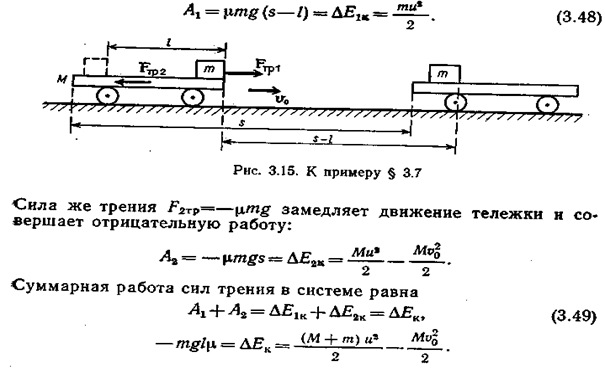
Из соотношения (3.49) видно, что изменение кинетической энергии системы равно работе силы трения на расстоянии, равном относительному перемещению тела вдоль тележки; кинетическая энергия системы убывает. Таким образом, хотя сила трения 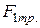 совершает положительную работу, суммарная работа сил трения отрицательна, она и приводит к уменьшению кинетической энергии системы.
совершает положительную работу, суммарная работа сил трения отрицательна, она и приводит к уменьшению кинетической энергии системы.
В любой системе, состоящей из макроскопических тел, реально действуют силы трения. Поэтому в замкнутой системе движущихся тел механическая энергия обязательно убывает. Но она не исчезает бесследно. Происходит переход механической энергии в тепловую. При работе сил трения тела нагреваются, или, как говорят, происходит увеличение их внутренней энергии.
12. СОУДАРЕНИЕ ДВУХ ТЕЛ
Соударением двух тел называется кратковременное взаимодействие тел. Рассмотрим два предельных вида соударения: абсолютно упругий и абсолютно неупругий удары. Абсолютно упругим называется такой удар, при котором на первой стадии кинетическая энергия полностью или частично переходит в потенциальную энергию упругой деформации, а на второй стадии тела восстанавливают первоначальную форму, отталкивают друг от друга. В результате потенциальная энергия упругой деформации снова переходит в кинетическую энергию. При абсолютно упругом ударе механическая энергия не переходит в другие, немеханические, виды энергии.
При абсолютно неупругом ударе потенциальной энергии деформации не возникает; кинетическая энергия полностью или частично превращается во внутреннюю энергию. После удара столкнувшиеся тела либо останавливаются, либо движутся с одинаковой скоростью. При абсолютно неупругом ударе выполняется закон сохранения количества движения и не выполняется закон сохранения механической энергии.
Рассмотрим абсолютно неупругий удар двух частиц, составляющих изолированную систему. Пусть массы частиц m1 и m2, а скорости до удара v1 и v2. Найдем их скорость после удара 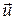 . На основании закона сохранения количества движения можем записать
. На основании закона сохранения количества движения можем записать
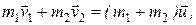 (12.1)
(12.1)
откуда
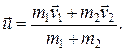 (12.2)
(12.2)
В качестве примера абсолютно неупругого соударения тел можно рассмотреть удар молота по поковке, которая находится на наковальне. В этом случае нужно, чтобы максимальное количество кинетической энергии молота было затрачено на деформацию поковки, т. е. кинетическая энергия молота и поковки с наковальней была минимальной.
Для того чтобы выяснить, как лучше выполнить это условие, вычислим изменение кинетической энергии системы при ударе. Пусть масса поковки с наковальней m1, и они неподвижны до удара (v1 = 0). Масса молота m2, и его скорость до удара v2. Изменение кинетической энергии системы в результате удара
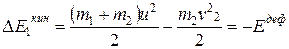 , (12.3)
, (12.3)
отсюда
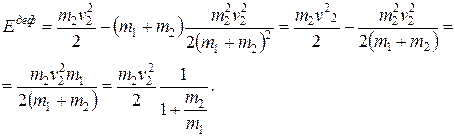 (12.4)
(12.4)
Из полученного выражения видно, что на деформацию будет израсходована тем большая часть кинетической энергии молота  чем масса наковальни (с поковкой) больше массы молота.
чем масса наковальни (с поковкой) больше массы молота.
Рассмотрим теперь абсолютно упругий удар двух шаров. При этом ограничимся только центральным ударом. Удар называется центральным, если шары до удара движутся вдоль прямой, проходящей через их центры.
Пусть масса шаров m1 и m2, скорости шаров до удара  и
и  , а после удара -
, а после удара -  и
и 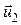 . Так как все векторы направлены вдоль одной прямой, мы в дальнейшем будем рассматривать скорости как алгебраические величины. Так как при абсолютно упругом соударении выполняются и закон сохранения механической энергии, и закон сохранения количества движения, можно записать систему уравнений:
. Так как все векторы направлены вдоль одной прямой, мы в дальнейшем будем рассматривать скорости как алгебраические величины. Так как при абсолютно упругом соударении выполняются и закон сохранения механической энергии, и закон сохранения количества движения, можно записать систему уравнений:
 ; (12.5)
; (12.5)
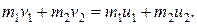 (12.6)
(12.6)
Для того чтобы найти величины скоростей шаров после удара, преобразуем уравнения:
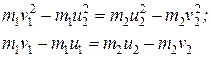 (12.7)
(12.7)
или
m1(v12 - u12) = m2(u22 - v22) (12.8)
m1(v1 - u1) = m2(u2 - v2).
Разделив почленно первое уравнение на второе, получим:
v1 + u1 = u2 + v2. (12.9)
Решив это уравнение совместно со вторым уравнением системы, получим:
 (12.10)
(12.10)
Рассмотрим некоторые частные случаи.
а) Массы шаров одинаковы m1 = m2. В этом случае получаем u1 = v2,u2 = v1, т.е. шары в результате соударения обмениваются скоростями.
в) Удар шара о неподвижную (v 2 = 0) стенку, которую можно рассматривать как шар бесконечно большого радиуса и очень большой массы(m2 >> m1). В этом случае получаем
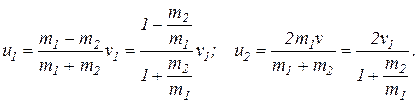 (12.11)
(12.11)
Учитывая, что 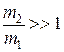 , получим:
, получим:
u1 » - v1; u2» 0. (12.12)
Шар при ударе о неподвижную стену изменяет скорость на противоположную, а стенка остается неподвижной.
7. ЗАКОН СОХРАНЕНИЯ ИМПУЛЬСА.
Рассмотрим систему N взаимодействующих меду собой частиц. Пусть на любую из частиц помимо сил взаимодействия 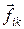 действуют внешние силы, результирующая которых равна
действуют внешние силы, результирующая которых равна  .
.
Для всех N частиц запишем уравнения второго закона Ньютона:
 (7.1)
(7.1)

………………………………………
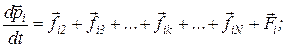
………………………………………
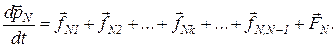
Сложим почленно эти равенства. В соответствии с третьим законом Ньютона 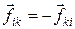 (
(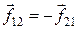 и т. д.). Поэтому после сложения равенств в правой части останется только сумма внешних сил:
и т. д.). Поэтому после сложения равенств в правой части останется только сумма внешних сил:
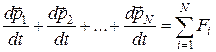 (7.2)
(7.2)
или
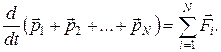 (7.3)
(7.3)
Сумма импульсов частиц
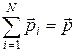 (7.4)
(7.4)
называется импульсом системы
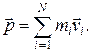 (7.5)
(7.5)
С учетом введенных обозначений запишем
 . (7.6)
. (7.6)
Если на частицы системы не действует внешние силы
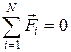 , (7.7)
, (7.7)
то импульс такой системы остается постоянным. Такая система называется изолированной, или замкнутой. Таким образом, мы пришли к формулировке закона сохранения количества движения (импульса): импульс изолированной системы частиц остается постоянным. Внутренние силы не в состоянии изменить импульс системы тел.
Следует отметить, что импульс системы остается постоянным и для неизолированной системы, если векторная сумма всех внешних сил равна нулю. Если проекция суммы внешних сил на некоторое направление равна нулю, то составляющая импульса системы на это направление постоянна.
 |
Пример 1. Бильярдный шарик массы m, движущийся по горизонтальной идеально гладкой поверхностью со скоростью
 , ударяется о преграду под углом
, ударяется о преграду под углом  к горизонту. Скорость шарика до удара и после удара имеет одну и ту
к горизонту. Скорость шарика до удара и после удара имеет одну и ту
Рис.7.1.
же величину, и угол падения равен углу отражения (рис. 7.1,а). Изменится ли импульс шарика?
Изменение импульса шарика 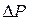 определяется:
определяется:
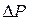 =
= .
.
Из рисунка видно, что изменение вектора  не равно нулю, следовательно, импульс шарика не сохраняется. Это происходит потому, что на него со стороны стенки действуют внешняя сила — сила упругости Fy, которая и меняет направление скорости шарика:
не равно нулю, следовательно, импульс шарика не сохраняется. Это происходит потому, что на него со стороны стенки действуют внешняя сила — сила упругости Fy, которая и меняет направление скорости шарика:
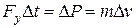
Импульс силы упругости направлен в ту же сторону, что и вектор изменения скорости  . Модуль импульса силы определяется из геометрического построения.
. Модуль импульса силы определяется из геометрического построения.
Пример 2. По рельсам без трения с постоянной скоростью движется платформа с закрепленным на ней орудием. Из орудия производят выстрел в направлении движения. Скорость снаряда относительно платформы, движущейся со скоростью 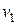 , равна и. Платформа продолжает двигаться в том же направлении со скоростью
, равна и. Платформа продолжает двигаться в том же направлении со скоростью  . Определить отношение масс снаряда и платформы.
. Определить отношение масс снаряда и платформы.
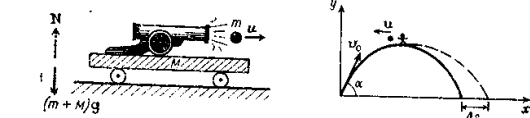 |
Рассмотрим систему тел платформа — снаряд.
| Рис.7.2. | Рис.7.3. |
На систему действуют внешние силы: сила тяжести и реакция опоры (рис. 7.2.). Однако вдоль горизонтального направления проекции этих сил равны нулю, поэтому вдоль этого направления импульс системы до и после выстрела остается неизменным. При решении задачи следует помнить, что значение всех скоростей, входящих в закон сохранения импульса, должны отсчитываться в одной и той же системе отсчета. Предложенную задачу можно рассмотреть в системе отсчета, связанной с Землей, или в системе отсчета, связанной, например, с платформой, движущейся с постоянной скоростью 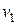 . Приведем оба решения.
. Приведем оба решения.
В системе координат, связанной с Землей, импульс системы платформа — снаряд до выстрела в горизонтальном направлении равен:
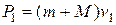
После выстрела
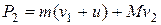
Согласно закону сохранения импульса  или
или

В системе координат, связанной с платформой, движущейся со скоростью 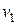 , импульс системы до выстрела равен нулю
, импульс системы до выстрела равен нулю
 =0
=0
После выстрела
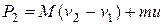
Так как импульс системы не изменяется, то  или
или

Следовательно

Таким образом, мы получили тот же ответ.
Пример 3. Акробат с мячом прыгает под углом  к горизонту с некоторой скоростью
к горизонту с некоторой скоростью  (рис. 7.3). В наивысшей точке своей траектории он бросает мяч назад с относительной скоростью и. Насколько увеличится дальность полета акробата?
(рис. 7.3). В наивысшей точке своей траектории он бросает мяч назад с относительной скоростью и. Насколько увеличится дальность полета акробата?
На систему тел акробат — мяч действует внешняя сила (сила тяжести). Однако вдоль горизонтального направления проекция силы тяжести равна нулю, поэтому можно записать закон сохранения импульса вдоль этого направления. Импульс системы акробат — мяч удобно записать в системе координат, связанной с акробатом. Ось ох направим горизонтально. В этой системе импульс тел до броска Р 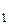 =0, после броска — в проекции на ось ОХ:
=0, после броска — в проекции на ось ОХ:
Р 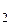 =
=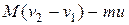 , где
, где 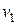 и
и  — горизонтальные составляющие скорости акробата до и после броска соответственно. Закон сохранения импульса вдоль направления оси ох имеет вид Р
— горизонтальные составляющие скорости акробата до и после броска соответственно. Закон сохранения импульса вдоль направления оси ох имеет вид Р 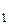 = Р
= Р 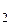 , или
, или
0=
Вычисленное из этого соотношения приращение скорости 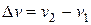 позволит определить, насколько увеличилась дальность полета акробата
позволит определить, насколько увеличилась дальность полета акробата
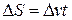
где t – время приземления акробата от верхней точки траектории.
Из раздела «Кинематика» при изучении движения тел, брошенных под углом  к горизонту, следует, что
к горизонту, следует, что
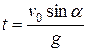
Следовательно, дальность полета акробата увеличится на
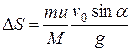 .
.
ЦЕНТР МАСС.
Центром масс (или центром инерции) системы называется точка С, положение которой задается радиусом - вектором 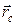 , определяемым следующим образом:
, определяемым следующим образом:
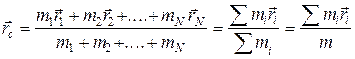 . (7.8)
. (7.8)
Здесь mi - масса i -й материальной точки, на которые мысленно разбито твердое тело, 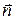 - радиус- вектор, определяющий положение этой материальной точки, m - масса всего тела, равная сумме масс всех материальных точек.
- радиус- вектор, определяющий положение этой материальной точки, m - масса всего тела, равная сумме масс всех материальных точек.
В однородном поле сил тяжести центр масс совпадает с центром тяжести системы.
Центр масс твердого тела движется так, как двигалось бы материальная точка с массой, равной массе тела, под действием всех приложенных к телу сил.
Второй закон Ньютона для центра масс можно записать
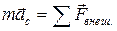 . (7.9)
. (7.9)
Это уравнение дает возможность установить движение центра масс твердого тела, если известна масса тела и действующие на него силы. В случае поступательного движения это уравнение будет определять ускорение не только центра масс, но и любой другой точки тела.
8. УРАВНЕНИЕ ДВИЖЕНИЯ ТЕЛА ПЕРЕМЕННОЙ МАССЫ.
Рассмотрим примеры использования закона сохранения импульса для объяснения некоторых явлений.
В повседневной жизни существуют такие явления, в которых при движении изменяется не только скорость, но и масса тела. Подобное движение совершает автомобиль, поливающий улицу, ракета, выбрасывающая струю сгоревших газов, и т. д. Общие законы движения тел с переменной массой были разработаны Мещерским и Циолковским. Циолковский применил эти законы движения для разработки технического проекта реактивного космического корабля. Рассмотрим движение ракеты.
Рис.8.1.
 |
При сжигании топлива в камере сгорания развивается высокое давление, и продукты сгорания выталкиваются наружу с некоторой скоростью относительно ракеты. Сама ракета получает приращение скорости. После выброса продукты сгорания перестают взаимодействовать с ракетой.
Выброшенные газы и ракету можно рассматривать как систему из двух тел, взаимодействующих между собой во время движения.
Будем полагать, что ракета массой М в некоторый момент времени движется со скоростью v (рис. 8.1). В единицу времени сгорает  топлива и выбрасывается наружу со скоростью и относительно самой ракеты. Относительно Земли это количество топлива будет иметь скорость (v+u). Масса ракеты спустя время
топлива и выбрасывается наружу со скоростью и относительно самой ракеты. Относительно Земли это количество топлива будет иметь скорость (v+u). Масса ракеты спустя время  станет равной
станет равной 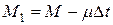 , а ее скорость в результате выброса некоторого количества топлива увеличится до значения
, а ее скорость в результате выброса некоторого количества топлива увеличится до значения 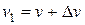 . На систему выброшенный газ — ракета при движении ракеты в горизонтальном направлении не действуют внешние силы. Поэтому вдоль этого направления выполняется закон сохранения импульса
. На систему выброшенный газ — ракета при движении ракеты в горизонтальном направлении не действуют внешние силы. Поэтому вдоль этого направления выполняется закон сохранения импульса
 ,
,
или
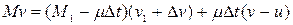
Раскрывая скобки, получим

Членом 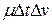 обычно пренебрегают по сравнению с остальными, так как он равен произведению двух малых величин
обычно пренебрегают по сравнению с остальными, так как он равен произведению двух малых величин  и
и  .
.
Тогда
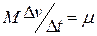 и или
и или  и.
и.
Это – уравнение Мещерского для движения тела с переменной массой.
Правая часть уравнения является реактивной силой, действующей на ракету со стороны газов. Как видно, она определяется скоростью истечения газов относительно ракеты и быстротою выгорания топлива, т.е. той массой газов, которая сгорает в единицу времени. Формула Мещерского является основой для расчета силы тяги ракетных и реактивных двигателей всех систем.
19. ДЕФОРМАЦИЯ И СИЛЫ УПРУГОСТИ
Кроме сил трения, при непосредственном соприкосновении тел могут возникать еще силы упругости. Для того, чтобы одно тело могло действовать на другое при контакте, действующее тело должно находиться в особом состоянии: например, чтобы рука действовала на предмет, мышцы руки должны сокращаться; чтобы действовать на пробку игрушечного пистолета, воздух или пружина должны быть сжаты. Сжатия, растяжения, изгибы – это примеры изменения формы или объема тел по сравнению с их исходным состоянием. Такие изменения называются деформациями.
Для того чтобы возникли силы упругости между телами или между отдельными частями одного и того же тела, необходимо, чтобы тела были деформированы.
Таким образом, силы упругости — это силы, возникающие только при деформации тел. При прекращении деформации силы упругости исчезают.
Различают два предельных случая деформации тела: упругие и пластические.
Деформация называется упругой, если после прекращения здешнего воздействия тело полностью восстанавливает свою форму и размеры. При пластической деформации изменения размеров и формы тела полностью не исчезают после прекращения действия силы.
Рассмотрим деформацию в упругих телах, т. е. таких телах, в которых возникают силы упругости, восстанавливающие полностью форму и объем тела после прекращения действия сил, вызывающих деформацию.
При деформации различные части тела испытывают различные перемещения. Например, если растягивать пружину, прикрепленную одним концом к неподвижной опоре некоторой внешней силой F, то эта сила сообщает ускорение не всем элементам пружины одновременно, а лишь какой-то ее части. Жесткая опора препятствует заметным перемещениям элементов, находящихся около нее, поэтому пружина оказывается деформированной. Относительное смещение элементов пружины продолжается до тех пор, пока деформация не приведет к появлению сил упругости, препятствующих дальнейшему перемещению частей тела.
Английский физик Роберт Гук установил экспериментальную зависимость между силой упругости и величиной деформации при сравнительно малых деформациях: деформация прямо пропорциональна приложенной силе.
 (19.1)
(19.1)
Это и есть закон Гука. Коэффициент пропорциональности k называется коэффициентом упругости (или жесткости) пружины. Учитывая, что ось ох и проекция силы упругости на эту ось имеют противоположные знаки, можно записать
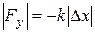 (19.2)
(19.2)
Коэффициент упругости для различных тел зависит от формы и материала вещества, в котором возникают силы упругости; его размерность согласно формуле (19.2) [ ]=Н/м. В пределах применимости закона Гука коэффициент k не должен зависеть от величины приложенной силы.
]=Н/м. В пределах применимости закона Гука коэффициент k не должен зависеть от величины приложенной силы.
Аналогичная закономерность наблюдается при растяжении стержней из стали, чугуна, алюминия и других твердых упругих тел. При сжатии стержней уменьшение их длины также пропорционально приложенной силе. Величина коэффициента упругости для стержней зависит не только от материала стержня, но и от его начальной длины 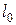 и площади поперечного сечения S. Эта зависимость отражается следующей формулой:
и площади поперечного сечения S. Эта зависимость отражается следующей формулой:
 (19.3)
(19.3)
Коэффициент Е называют модулем упругости материала, или модулем Юнга. Он уже не зависит от размеров тела. Сила же упругости для стержня будет равна
 (19.4)
(19.4)
Следует отметить, что при деформации твердых тел некоторой внешней силой F нельзя переносить эту силу вдоль линии ее действия. Между силами и вызванными ими деформациями в общем случае существует весьма сложная связь.
|
|
|
|
|
Дата добавления: 2014-01-11; Просмотров: 968; Нарушение авторских прав?; Мы поможем в написании вашей работы!
