КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
II. Основы молекулярной физики и термодинамики
|
|
|
|
1. МОЛЕКУЛЯРНО-КИНЕТИЧЕСКИЕ ПРЕДСТАВЛЕНИЯ О ВЕЩЕСТВЕ
Механика изучает движения и взаимодействия макроскопических тел, не интересуясь их внутренним строением и предполагая, что тела являются системами материальных точек, неподвижных относительно друг друга и жестко связанных между собой, например, модель абсолютно твердого тела.
Молекулярная физика рассматривает явления, происходящие внутри макроскопических тел, т.е. изучает те свойства вещества, которые обусловлены его внутренним строением. В молекулярной физике принимается, что вещество имеет молекулярно-кинетическое строение. Основные положения современной молекулярно-кинетической теории вещества следующие:
1) Все тела состоят из мельчайших частиц-атомов и молекул.
2) Атомы и молекулы находятся в состоянии непрерывного движения. Это хаотическое движение называется тепловым движением.
3) Молекулы различных веществ по-разному взаимодействуют между собой. Это взаимодействие существенно зависит от типа молекул и от расстояний между ними.
Таким образом, в молекулярной физике структурными частицами вещества являются не материальные точки, а атомы и молекулы. Чем отличается материальная точка от атомов и какая разница между ними? Материальная точка - это маленький кусочек тела, размеры которого многократно меньше по сравнению с расстоянием до других точек. Материальная точка обладает массой, атомы и молекулы тоже имеют массу.
В молекулярной физике атом - это наименьшая частица химического элемента, он является носителем всех свойств данного элемента. Масса атома одного элемента отличается от массы атома другого элемента.
Молекула - это наименьшая частица вещества, носитель всех свойств этого вещества. Молекула - более крупная частица, состоит из одного или нескольких атомов.
Для характеристики масс атомов и молекул вводится специальная эталонная масса, равная 1/12 части массы атома углерода и называется атомной единицей массы (а.е.м.)  . Массы атомов и молекул других химических элементов и веществ определяются путем сравнения с атомной единицей массы (а.е.м.).
. Массы атомов и молекул других химических элементов и веществ определяются путем сравнения с атомной единицей массы (а.е.м.).
Относительной атомной массой химического элемента называется отношение массы атома этого элемента к а.е.м., т.е.
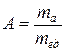 (безразмерная величина). (1.1)
(безразмерная величина). (1.1)
Относительной молекулярной массой М вещества называется отношение массы молекулы этого вещества к 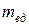 , т.е.
, т.е.
 (безразмерная величина). (1.2)
(безразмерная величина). (1.2)
Следовательно, масса атома 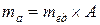 , масса молекулы
, масса молекулы 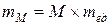 .
.
В молекулярной физике вводится еще одна единица, называемая молем, т.е. единица количества вещества. Если взять какого-либо вещества в количестве одного моля, то число частиц этого вещества столько же, что и атомов в 12 граммах углерода. Число частиц (атомов, молекул, ионов и др.), содержащихся в одном моле вещества, называется постоянной Авогадро:
 .
.
Масса вещества в количестве одного моля называется молярной массой 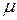
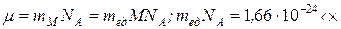 6,022.1023 =
6,022.1023 =
=0,999652 г/моль ~ 1, т.е.  .
.
Равенство  означает, что относительная молекулярная масса вещества М, выраженная в граммах, численно равна молярной массе вещества
означает, что относительная молекулярная масса вещества М, выраженная в граммах, численно равна молярной массе вещества 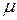 .
.
Введенные величины позволяют найти массу атома любого элемента или массу молекулы любого вещества. Например, для углерода масса атома 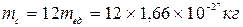 или
или
 (1.3)
(1.3)
Получив представление о массе молекул, произведем оценку их размеров. Предполагаем, что в жидкостях и твердых телах молекулы располагаются "вплотную" друг к другу. Поэтому, если разделим объем моля жидкости на число  , то получим объем, занимаемый одной молекулой. Проще всего это сделать для воды. Моль воды, т.е. 18 г, занимает 18
, то получим объем, занимаемый одной молекулой. Проще всего это сделать для воды. Моль воды, т.е. 18 г, занимает 18 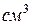 т.е.
т.е. 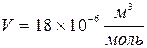 . На долю одной молекулы приходится объем, равный
. На долю одной молекулы приходится объем, равный
 .
.
Линейные размеры молекулы  . Если возьмем обратное отношение, то оно показывает концентрацию молекул:
. Если возьмем обратное отношение, то оно показывает концентрацию молекул:
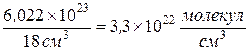 .
.
Движение молекул имеет место при всех трех состояниях вещества: при твердом состоянии молекулы движутся около положений равновесия. Это движение всей молекулы можно считать колебательным (линейным), но могут колебаться и составные части молекулы относительно друг друга и совершать вращательные колебания около центра тяжести молекулы. Поступательное движение молекул в твердом состоянии отсутствует. Молекулы имеют постоянное положение равновесия.
В жидком состоянии молекулы также совершают колебательное и вращательное движения, но не имеют постоянного положения равновесия. Это положение все время изменяется, т.е. в жидкости имеет место и поступательное движение молекул.
Согласно закону Авогадро при нормальных условиях (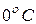 или 273,15 К и давление в одну атмосферу (1,013 ×105 Па) объем моля любого газа равен 22,4 л/моль=
или 273,15 К и давление в одну атмосферу (1,013 ×105 Па) объем моля любого газа равен 22,4 л/моль=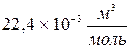 и содержит 6,022 × 1023 молекул, следовательно, в газах одна молекула занимает объем:
и содержит 6,022 × 1023 молекул, следовательно, в газах одна молекула занимает объем:
 .
.
Для молекул твердых тел и жидкостей -  . Таким образом, молекула газа занимает объем в
. Таким образом, молекула газа занимает объем в
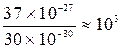
раза больше, чем молекула твердого или жидкого тела, а расстояние между молекулами газа  , т.е. в 10 раз больше, поэтому они слабо взаимодействуют.
, т.е. в 10 раз больше, поэтому они слабо взаимодействуют.
В разреженных газах молекулы удалены друг от друга настолько, что силы взаимодействия между ними практически отсутствуют. Молекулы газов движутся от столкновения до столкновения между собой или со стенками сосуда прямолинейно и равномерно. Это движение хаотично, т.е. в среднем в каждом направлении в любой момент времени движется одинаковое число молекул.
2. ИДЕАЛЬНЫЙ ГАЗ. ГАЗОВЫЕ ЗАКОНЫ.
Понятие "идеального газа" является определенной моделью вещества, которая вводится для объяснения свойств реального газа.
Идеальный газ представляют как систему свободных невзаимодействующих частиц, находящихся в непрерывном хаотическом движении.
Взаимодействия частиц проявляются только в их упругих столкновениях. Частицы идеального газа принимают за твердые шарики, размеры которых намного меньше среднего расстояния между ними. Благодаря беспорядочному движению частицы идеального газа очень часто сталкиваются друг с другом, и размениваясь энергией разлетаются в разные стороны, быстро рассеиваются в пространстве, занимая бесконечно большой объем. Поэтому в большинстве случаев идеальный газ рассматривают внутри некоторого объема. Частицы, встречая на своем пути стенки сосуда, будут упруго отражаться, передавая стенке определенное количество движения (импульс силы). Следствием этого является давление, оказываемое газом на стенку.
Гaз характepизyeтcя тpeмя пapaмeтpaми: oбъeмoм V, дaвлeнueм P и тeмnepaтyрой T. Teмпepaтypa мoжeт быть измepeнa пo paзным тeмпepaтypным шкaлaм - абсолютнaя тeмnepaтypa cвязaнa c тeмпepaтypoй пo шкaлe Цeльcия cooтнoшениeм: T = t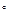 C + 273C.
C + 273C.
Еcли знaчeния тeмпepaтypы и дaвлeния в paзличныx тoчкax oбъeмa paзныe, то темпepaтypa и дaвлeниe являютcя фyнкциями кoopдинaт, т.e. T(x, y, z),Р(х y,z). B этoм cлyчae raз (cиcтeмa) нaxoдитcя в нepaвнoвecнoм cocтoянии и мы нe мoжeм нaзвaть знaчeния дaвлeния и тeмпepaтypы, oпpeдeляющиe coстояниe cиcтeмы. Ecли cиcтeмy, нaxoдящyюcя в нepaвнoвecнoм cocтoянии, пpeдоставить caмoй ceбe, тo тeмпepaтypa и дaвлeниe пocтeпeннo выpaвнивaютcя, системa пpиxoдит в paвнoвecнoe cocтoяниe. Paвнoвecнoe cocmoянue - этo coстояниe, пpи кoтopoм тeмпepaтypa и дaвлeниe вo вcex тoчкax oбъeмa oдинaкoвы. Состояниe гaзa мoжeт быть oпpeдeлeнo, ecли oн нaxoдитcя в paвнoвecнoм coстоянии.
На гpaфикax зaвиcимocти P - V, T-V и P - T мы мoжeм изoбpaжaть тoлько такие пpoцeccы, пpи кoтopыx кaждoe пpoмeжyтoчнoe cocтoянииe являeтcя равновecным. Taкиe пpoцeccы нaзывaютcя oбpaтuмы. Экcпepимeнтaльнo иcследовaлиcь пpoцeccы, пpи кoтopьrx oдин из тpex пapaмeтpoв и мacca гaзa ocтaвались нeизмeнными, Эти зaкoны нaзывaютcя гaзoвымu зaкoнaмu, и ecли гaз подчиняeтcя гaзoвым зaкoнaм, eгo мoжнo cчитaть uдeaльным (eщe oднo oпpeделение идeaльнoгo гaзa).
1. Закон Бoйля - Mapuoттa.
Для дaннoй мaccы гaзa пpи пocтoяннoй тeмператуpe пpoизвeдeниe дaвлeния нa oбъeм ocтaeтcя вeличинoй пocтoяннoй:
PV=const. (2.1.)
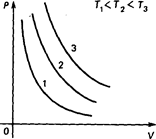
Pиc. 2.1.
Эта зависимость изображена на рис.2.1 Процeccы, пpoиcxoдящиe пpи пocтoяннoй тeмпepaтype, нaзывaютcя uзoтeмическuмu, a кpивыe, изoбpaжaющиe пpoцeccы пpи T = const, нaзывaютcя изотермами, Пocкoлькy P = C/V (C = const), изoтepмы являютcя гипepбoлaми.
2. Зaкoн Гeй-Люccaкa.
Для дaннoй мaccы гaзa пpи пocтoяннoм давлении

Pиc. 2.2.
oбъeм измeняeтcя пpи yвeличeнии тeмпepaтypы пo линeйнoмy зaкoнy:
V=Vo(l+at"C), (2.2)
гдe  = 1/2730C. Пoдcтaвив a в (2.2), пoлyчим
= 1/2730C. Пoдcтaвив a в (2.2), пoлyчим
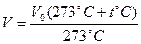 (2.3)
(2.3)
Bвeдeм aбcoлютнyю тeмпepaтypy T = 273° C + t"C, oткyдa
 (2.4)
(2.4)
Зaкoн Гeй-Люccaкa мoжнo cфopмyлиpoвaть cлeдyющим oбpaзoм: oтнoшeниe oбъeмa к aбcoлютнoй тeмпepaтype для дaннoй мaccы гaзa пpи пocтoяннoм дaвлeнии ocтaeтcя пocтoянным. Пpoцeccы, пpoиcxoдящиe пpи пocтoяннoм дaвлeнии, нaзывaютcя uзoбapнымu, a кpивыe, изoбpaжaющиe изoбapный пpoцecc, uзoбapaмu. Ha pиc.2.2 пoкaзaны двe изoбapы пpи paзличныx дaвлeнияx P < Pг, (oчeвиднo, чтo пpи дaннoй тeмпepaтype, чeм бoлыue oбъeм, тeм мeньшe дaвлeниe). Oкoлo тoчки t" > —273° C (T -- 0) зaвиcимocти изoбpaжeны пyнктиpными линиями. Этo пoнятнo, тaк кaк пpи низкиx тeмпepaтypax гaз пpeвpaщaeтcя в жидкocть и зaкoны, нaйдeнныe экcпepимeнтaльнo для гaзa, нe paбoтaют. Пpoдoлжив экcпepимeнтaльныe зaвиcимocти V(t"C) дo пepeceчeния c ocью aбcциcc, нaйдeм, чтo oни пepeceкaютcя в oднoй тoчкe - T = 0.
3. Зaкoн Шapля.
Для пocтoяннoй мaccы гaзa пpи пocтoяннoм oбъeмe oтнoшeниe дaвлeния гaзa к eгo тeмпepaтype ocтaeтcя пocтoянным:
P/T = const пpи m = const, V = const. (2.5)
Пpoцeccы, пpoиcxoдящиe пpи пocтояннoм oбъeмe, нaзывaютcя uзoxopнымu, и кpивыe иx изoбpaжaющиe — uзoxopaмu.
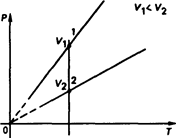
Ha pиc. 2.3 изoбpaжeны изoxopныe пpoцесcы пpи paзныx знaчeнияx oбъeмa. Зaвиcимocти вблизи aбcoлютнoгo нyля изoбpaжeны тaк жe, кaк и пpи изoбapныx пpoцeccax, пyнктиpными линиями. Укaзaнныe тpи зaкoнa ycтaнaвливaют cвязь двyx из тpex пapaмeтpoв гaзa.
4. Зaкoн Дaльтoнa.
Ecли в cocyдe oбъeмoм V нaxoдитcя cмecь гaзoв, тo дaвлeниe cмecи гaзoв paвнo cyммe пapциaльныx дaвлeний каждого газа:
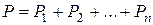 . (2.6)
. (2.6)
Пapцuaльнoe дaвлeнue — этo дaвлeниe кoмпoнeнты cмecи, ecли бы oнa зaнимaлa вecь oбъeм,
Aтмocфepнoe дaвлeниe тaкжe oпpeдeляeтcя cyммoй пapциaльныx дaвлeний кoмпoнeнтoв, из кoтopыx cocтoит вoздyx: киcлopoдa, yглeкиcлoгo гaзa, aзoтa, пapoв вoды.
3. УРАВНЕНИЕ КЛАЙПЕРОНА-МЕНДЕЛЕЕВА.
Уpaвнeниe, ycтaнaвливaющee cвязь вcex тpex пapaмeтpoв пpи пocтoяннoй мacce гaзa, нaзывaeтcя уравнением состояния идеального газа.
Пycть cиcтeмa, нaxoдящaяcя в cocтoянии 1 (pиc. 2.4), xapaктepизyющeмcя пapaмeтpaми P1,V1,T1, пepeшлa в cocтoяниe 2, xapaктepизyющeecя пapaмeтpaми P2,V2,T2. Пepeвeдeм cиcтeмy из cocтoяния 1 в 2 cлeдyющим образом: гaз изoтepмичecки pacшиpяeтcя дo oбъeмa Vг (кpивaя 1 - 1), a зaтeм изoxopнo нaгpeвaeтcя дo тeмпepaтypы Ty (oтpeзoк 1’ - 2). Итaк, пpoмeжyтoчнoe
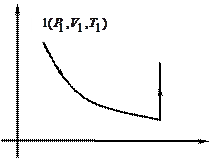
|
|
|
 0 V
0 V
Pиc.2.3. Рис.2.4
cocтoяниe гaзa 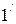 xapaктepизyeтcя пapaмeтpaми
xapaктepизyeтcя пapaмeтpaми 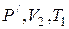 . Пpи изoтepмичecкoм pacшиpeнии cпpaвeдливo выpaжeниe
. Пpи изoтepмичecкoм pacшиpeнии cпpaвeдливo выpaжeниe
 - (зaкoн Бoйля — Mapиoттa) (3.1)
- (зaкoн Бoйля — Mapиoттa) (3.1)
Пpи изoxopнoм нaгpeвaнии
 (зaкoн Шapля) (3.2)
(зaкoн Шapля) (3.2)
Bыpaзив  из этих выражений и приравняв их, получим:
из этих выражений и приравняв их, получим:
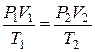 , (3.3)
, (3.3)
т.е., при 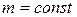
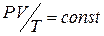 (3.4)
(3.4)
Это уpaвнeниe Kлaпeйpoнa — Meндeлeeвa, или ypaвнeниe cocтoяния идeaльнoгo гaзa, cвязывaeт тepмoдинaмичecкиe пapaмeтpы и мaccy гaзa.
Извecтнo, чтo 1 мoль любoгo гaзa пpи нopмaльныx ycлoвияx (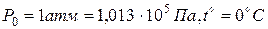 или
или 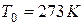 ) зaнимaeт oбъeм Vo = 22,4 л. Для oднoгo мoля мoжнo зaпиcaть ypaвнeниe:
) зaнимaeт oбъeм Vo = 22,4 л. Для oднoгo мoля мoжнo зaпиcaть ypaвнeниe:
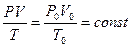 (3.5)
(3.5)
Beличинa R = PoVo/To нaзывaeтcя yнuвepcaльнoй (oдинaкoвoй для вcex гaзoв) гaзoвoй nocmoяннoй:

Итaк,
PV/T = R, или PV = RT (3.6)
Ecли в oбъeмe V coдepжитcя m/M мoлeй, тo
PV = (m/M)RT (3.7)
— ypaвнeниe Kлaпeйpoнa — Meндeлeeвa. Bce вышe пepeчиcлeнныe гaзoвыe зaкoны являютcя чacтным cлyчaeм ypaвнeния Kлaпeйpoнa — Meндeлeeвa, Гaзoвaя пocтoяннaя R cвязaнa c чиcлoм Aвoгaдpo и пocтoяннoй Бoльцмaнa k:
 (3.8)
(3.8)
гдe k = 1,38  Дж/K- постоянная Больцмана.
Дж/K- постоянная Больцмана.
Пoдcтaвив этo выpaжeниe в уравнение Клапейрона-Менделеева, пoлyчим
PV = NkT, (3.9)
гдe N - чиcлo мoлeкyл гaзa
Beличинa 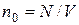 нaзывaeтcя кoнцeнmpaцueй мoлeкyл.
нaзывaeтcя кoнцeнmpaцueй мoлeкyл.
Taким oбpaзoм,
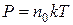 (3.10)
(3.10)
эти уpaвнeния нaзывaютcя ypaвнeнuямu cocmoянuя uдeaльнoгo гaзa.
4. СРЕДНЯЯ ЭНЕРГИЯ МОЛЕКУЛ ИДЕАЛЬНОГО ГАЗА
Рассмотрим неподвижный объем V, заполненный идеальным газом. Масса молекулы m, общее число молекул N, газ находится в состоянии равновесия, т.е. при постоянной температуре. Ввиду того, что газ считается идеальным, молекулы его будут отличаться друг от друга только своим положением в объеме и характером движения. Сказанное означает, что каждая молекула в объеме будет двигаться со своей скоростью 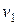 , отличающейся от скоростей других молекул и по модулю, и по направлению. Следовательно, каждая молекула будет обладать кинетической энергией, равной
, отличающейся от скоростей других молекул и по модулю, и по направлению. Следовательно, каждая молекула будет обладать кинетической энергией, равной  , а полная энергия данного объема идеального газа U будет равна сумме кинетических энергий всех его молекул:
, а полная энергия данного объема идеального газа U будет равна сумме кинетических энергий всех его молекул:
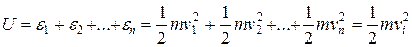 . (4.1)
. (4.1)
Однако, сталкиваясь друг с другом, молекулы непрерывно обмениваются энергией, в результате энергии различных молекул мало отличаются от некоторого среднего значения энергии, определяемого выражением:.
 . (4.2)
. (4.2)
Величина  представляет собой среднее значение квадрата скорости молекул. Извлекая из этого выражения квадратный корень, получим величину, называемую средней квадратичной скоростью молекул. Таким образом, полная энергия идеального газа объемом V может быть вычислена по формуле
представляет собой среднее значение квадрата скорости молекул. Извлекая из этого выражения квадратный корень, получим величину, называемую средней квадратичной скоростью молекул. Таким образом, полная энергия идеального газа объемом V может быть вычислена по формуле  .
.
Отметим, что замена точных значений скоростей молекул одной среднеквадратичной скоростью (по модулю) приводит к тому, что в некоторых случаях численные значения определяемых физических величин могут отличаться от истинных на 10-20%.
5. ДАВЛЕНИЕ ГАЗА
Совершая беспорядочные движения, молекулы газа приближаются к стенкам сосуда на достаточно малые расстояния. Точно так же молекулы могут подойти достаточно близко друг к другу. Происходит столкновение молекул, в результате которого молекулы изменяют направление своего движения.
Из-за столкновения молекул со стенками сосуда газ действует на стенки с определенной силой, которая тем больше, чем больше площадь поверхности стенок сосуда. Для характеристики свойства газа удобно пользоваться понятием силы, отнесенной к единице площади поверхности. Эта сила называется давлением:
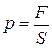 . (5.1)
. (5.1)
Свойство газа оказывать давление на стенки содержащего его сосуда - одно из основных его свойств. Давление газа на стенки сосуда является следствием бесчисленных столкновений молекул со стенками. Это предположил еще в 18 веке Даниил Бернулли. Удары молекул о стенки приводят к некоторым смещениям частиц материала стенки, т.е. к ее деформации. Деформированная стенка действует на газ упругой силой, направленной в каждой точке перпендикулярно к стенке. Сила эта равна по абсолютному значению и противоположна по направлению силе, с которой газ действует на стенку.
В системе СИ за единицу давления принимается Паскаль (Па) - такое давление, при котором на 1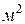 поверхности нормально к ней действует сила в 1 Ньютон;
поверхности нормально к ней действует сила в 1 Ньютон;
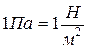 .
.
6. ОСНОВНОЕ УРАВНЕНИЕ МОЛЕКУЛЯРНО-КИНЕТИЧЕСКОЙ
ТЕОРИИ ГАЗОВ
Подсчитаем давление, возникающее в результате удара молекул о стенки сосуда. Для удобства сосуд представим себе в виде куба с длиной ребра 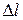 внутри которого беспорядочно двигаются N молекул (рис.6.1). Ввиду полной беспорядочности движения молекул результат их ударов будет таков, как если бы 1/3 всех молекул двигалась вдоль оси Х, 1/3 вдоль оси Y и 1/3 -вдоль оси Z. В результате удара импульс одной молекулы, летящей со скоростью
внутри которого беспорядочно двигаются N молекул (рис.6.1). Ввиду полной беспорядочности движения молекул результат их ударов будет таков, как если бы 1/3 всех молекул двигалась вдоль оси Х, 1/3 вдоль оси Y и 1/3 -вдоль оси Z. В результате удара импульс одной молекулы, летящей со скоростью 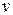 , изменится на величину
, изменится на величину  , где
, где  - масса молекул, с другой стороны согласно закону об изменении импульса можно написать:
- масса молекул, с другой стороны согласно закону об изменении импульса можно написать: 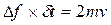 где
где 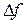 - сила удара,
- сила удара, 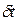 - продолжительность удара.
- продолжительность удара.
Отскочив от стенки, молекула полетит к противоположной стенке и отскочив, в свою очередь, от нее снова вернется к первой стенке. Пусть это происходит за время 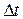 , а средняя сила удара
, а средняя сила удара 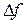 , т.е.
, т.е. 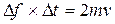 .
.
Фактически интервал времени 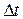 представляет собой время, необходимое молекуле, чтобы пролететь двойное расстояние между гранями куба
представляет собой время, необходимое молекуле, чтобы пролететь двойное расстояние между гранями куба 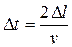 . Подставляя это значение для
. Подставляя это значение для 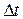 в предыдущую формулу, имеем
в предыдущую формулу, имеем
 . (6.1)
. (6.1)
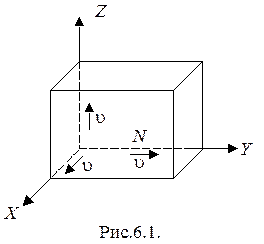
Разные молекулы движутся с разными скоростями 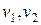 . Тогда средняя сила удара всех молекул, летящих в одном направлении
. Тогда средняя сила удара всех молекул, летящих в одном направлении
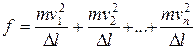 . (6.2)
. (6.2)
где n¢ - число молекул, летящих в одном направлении, равное
 . (6.3)
. (6.3)
Отсюда, вынося за скобки  , умножая и деля на n¢, получаем
, умножая и деля на n¢, получаем
 . (6.4)
. (6.4)
Величина 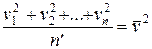 представляет собой среднее значение квадратов скоростей молекул. Преобразуя далее, получаем:
представляет собой среднее значение квадратов скоростей молекул. Преобразуя далее, получаем:
 . (6.5)
. (6.5)
Поделив правую и левую части этого равенства на 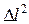 , получим:
, получим:
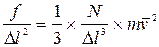 . (6.6)
. (6.6)
Здесь 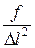 - давление на стенку куба,
- давление на стенку куба, 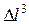 - объем.
- объем. 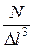 = n - число молекул в единице объема.
= n - число молекул в единице объема.
Окончательно последнее равенство может быть записано
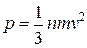 (6.7)
(6.7)
или, заменяя 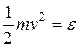 , имеем
, имеем 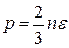 .
.
Полученное соотношение называется основным уравнением молекулярно-кинетической теории идеального газа, или уравнением Клаузиуса.
Для практического использования это уравнение является неудобным, ибо измерять непосредственно величину энергии 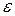 невозможно. Преобразуем его так, чтобы входящие физические величины подлежали непосредственному наблюдению и измерению, т.е. были макроскопическими величинами.
невозможно. Преобразуем его так, чтобы входящие физические величины подлежали непосредственному наблюдению и измерению, т.е. были макроскопическими величинами.
Производя замену 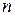 на
на 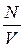 находим
находим
 . (6.8)
. (6.8)
Далее из определения средней энергии молекул можно получить
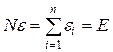 - cуммарную кинетическую энергию теплового движения всех молекул.
- cуммарную кинетическую энергию теплового движения всех молекул.
Имеем  , т.е. произведение объема газа на его давление численно равно 2/3 кинетической энергии всех молекул данного объема. Это соотношение связывает макроскопически наблюдаемые и измеряемые величины p и V с основной характеристикой микроскопических движений молекул внутри газа.
, т.е. произведение объема газа на его давление численно равно 2/3 кинетической энергии всех молекул данного объема. Это соотношение связывает макроскопически наблюдаемые и измеряемые величины p и V с основной характеристикой микроскопических движений молекул внутри газа.
Если массу газа с объемом V обозначим через М, то число грамм-молекул в этом объеме будет равно отношению 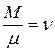 . Число молекул в одном моле любого вещества одно и то же. Эту величину называют числом Авогадро и обозначают NA. Общее число молекул в объеме V с использованием вышеназванных величин, будет
. Число молекул в одном моле любого вещества одно и то же. Эту величину называют числом Авогадро и обозначают NA. Общее число молекул в объеме V с использованием вышеназванных величин, будет
 . (6.9)
. (6.9)
Используя полученное выражение, преобразуем основное уравнение:
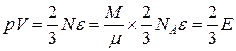 . (6.10)
. (6.10)
Сопоставим это уравнение с эмпирическим уравнением Менделеева-Клапейрона для того же числа молей,
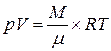 . (6.11)
. (6.11)
Получим  , таким образом, полная энергия идеального газа прямо пропорциональна его абсолютной температуре.
, таким образом, полная энергия идеального газа прямо пропорциональна его абсолютной температуре.
Преобразуем это уравнение с цель определения средней кинетической энергии одной молекулы
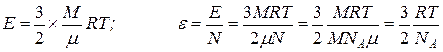 . (6.12)
. (6.12)
Величины R и 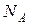 являются универсальными постоянными. Их отношение
являются универсальными постоянными. Их отношение 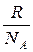 также является постоянной величиной, носит название постоянной Больцмана и обозначается буквой
также является постоянной величиной, носит название постоянной Больцмана и обозначается буквой 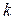 .
.
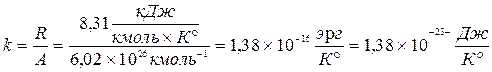 .
.
Вводя постоянную Больцмана, имеем
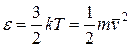 . (6.13)
. (6.13)
Из уравнения видно, что абсолютная температура непосредственно связана со средней кинетической энергией молекул. Эту энергию мы условились использовать в качестве характеристики теплового движения молекул, т.е. считали мерой интенсивности теплового движения молекул. Оказывается, как это видно из уравнения, количественное значение средней энергии молекулы однозначно определяется величиной температуры. Таким образом, из уравнения вытекает молекулярно-кинетический смысл понятия температуры.
Температура тела - это есть количественная мера энергии теплового движения его молекул.
Из уравнения  также следует, что при одинаковой температуре кинетические энергии молекул всех газов одинаковы, т.е. энергия молекулы не зависит от ее массы.
также следует, что при одинаковой температуре кинетические энергии молекул всех газов одинаковы, т.е. энергия молекулы не зависит от ее массы.
С помощью уравнения (6.13) можно вычислить среднюю квадратичную скорость:
 (6.14)
(6.14)
Ecли бы вce мoлeкyлы гaзa двигaлиcь co cpeднe-квaдpaтичнoй cкopocтью, тo дaвлeниe и тeмпepaтypa тaкoгo raзa были бы тaкими жe, кaк y peaльнoгo гaзa. Cpeднe-квaдpaтичнaя cкopocть oпpeдeляeт тepмoдинaмичecкиe пapaмeтpы — дaвлeниe и тeмпepaтypy.
Используя соотношение  можно преобразовать основное уравнение молекулярно-кинетической теории газов к виду:
можно преобразовать основное уравнение молекулярно-кинетической теории газов к виду:
 . (6.15)
. (6.15)
В таком виде это уравнение связывает давление газа p с концентрацией молекул n и абсолютной температурой Т.
7. СКОРОСТИ МОЛЕКУЛ ГАЗА. МАКСВЕЛЛОВСКОЕ РАСПРЕДЕЛЕНИЕ МОЛЕКУЛ ПО СКОРОСТЯМ
Согласно кинетической теории газов молекулы совершают хаотическое движение, их скорости различны и по величине и по направлению. Среди них имеются как очень быстрые, так и очень медленные, т.е. имеется какое-то распределение молекул по скоростям. Несмотря на беспорядочность молекулярных движений, случайный характер их столкновений и вызываемых ими изменений скорости молекул, их распределение по скоростям, оказывается, имеет постоянный и вполне определенный характер.
Решить задачу о распределении молекул газа по скоростям - это значит установить закон, позволяющий определить какое число молекул dn из общего количества n молекул единичного объема газа обладает при данной температуре скоростями в интервале от 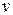 до
до 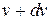 . Почему в интервале от
. Почему в интервале от 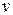 до
до 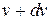 ? Дело в том, что вероятное число молекул, имеющих математически точно заданную скорость, равна нулю, т.к. число возможных значений скорости бесконечно велико, число же молекул конечно. Например, допустим, что требуется определить распределение населения страны по возрасту. Если мы будем искать число людей, имеющих математически точный возраст: 20 лет 3 мес. 5 мин. 2 сек, среди многочисленного населения страны может не оказаться ни одного человека с таким возрастом. Другое дело, если будем искать число людей, возраст которых находится между 18 и 18,5 годами. Их количество будет вполне определенным.
? Дело в том, что вероятное число молекул, имеющих математически точно заданную скорость, равна нулю, т.к. число возможных значений скорости бесконечно велико, число же молекул конечно. Например, допустим, что требуется определить распределение населения страны по возрасту. Если мы будем искать число людей, имеющих математически точный возраст: 20 лет 3 мес. 5 мин. 2 сек, среди многочисленного населения страны может не оказаться ни одного человека с таким возрастом. Другое дело, если будем искать число людей, возраст которых находится между 18 и 18,5 годами. Их количество будет вполне определенным.
Следовательно, вопрос ставится так: сколько молекул или какая часть молекул обладает скоростями, лежащими в некотором интервале вблизи заданной скорости.
Очевидно, что число dn частиц в единице объема, скорости которых лежат в интервале от 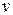 до
до 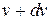 , тем больше, чем больше интервал, т.е.
, тем больше, чем больше интервал, т.е.
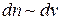 или
или 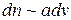 , (7.1)
, (7.1)
где 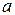 - коэффициент пропорциональности.
- коэффициент пропорциональности.
Ясно также, что dn зависит и от самой скорости, т.к. в одинаковых по величине интервалах, но при различных абсолютных значениях скорости число частиц будет различным.
Для пояснения вернемся к рассмотренному примеру. Например, неодинаковым будет число людей, имеющих возраст в интервале от 18 до 19 лет и от 100 до 101 года, хотя размеры интервалов в обоих случаях одинаковы.
Это значит, что в формуле коэффициент пропорциональности должен быть функцией скорости: 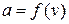 .
.
Наконец число 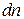 должно быть также пропорциональным числу частиц в единице объема
должно быть также пропорциональным числу частиц в единице объема 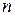 . Поэтому формула для величины
. Поэтому формула для величины 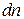 должна иметь вид:
должна иметь вид:
 . (7.2)
. (7.2)
Эту формулу обычно записывают в виде:
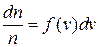 . (7.3)
. (7.3)
Величина  в этой формуле представляет собой долю частиц, скорости которых лежат в интервале от
в этой формуле представляет собой долю частиц, скорости которых лежат в интервале от 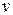 до
до 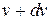 .
.
Функция 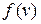 называется функцией распределения. Наша задача - найти вид этой функции. Смысл функции
называется функцией распределения. Наша задача - найти вид этой функции. Смысл функции 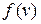 ясен из приведенной ранее формулы.
ясен из приведенной ранее формулы.
Действительно, при 
 . (7.4)
. (7.4)
Это значит, что 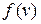 численно равна доле частиц, скорости которых лежат в единичном интервале скоростей вблизи скорости
численно равна доле частиц, скорости которых лежат в единичном интервале скоростей вблизи скорости 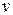 .
.
В формуле 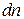 представляет число молекул, скорости которых лежат в интервале от
представляет число молекул, скорости которых лежат в интервале от 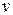 до
до 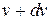 :
:
 . (7.5)
. (7.5)
Если суммировать все 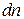 , соответствующие всем возможным значениям интервалов скоростей, то, очевидно, получится полное число частиц в единице объема
, соответствующие всем возможным значениям интервалов скоростей, то, очевидно, получится полное число частиц в единице объема 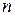 :
:
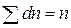 . (7.6)
. (7.6)
Функция распределения молекул по скоростям была найдена Максвеллом, носит его имя и имеет вид
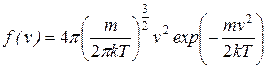 . (7.7)
. (7.7)
Как и можно было ожидать, конкретный вид функции зависит от рода газа (от массы молекулы) и от параметра состояния (от температуры Т).
График функции распределения выглядит так.

Из рис.7.1 видно, что функция обращается в нуль при  и при
и при 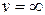 , т.е. число неподвижных молекул, как и число молекул, движущихся с очень большими скоростями равно нулю. Пользуясь кривой распределения Максвелла, можно графически определить число молекул, обладающих скоростями лежащими в заданном интервале между
, т.е. число неподвижных молекул, как и число молекул, движущихся с очень большими скоростями равно нулю. Пользуясь кривой распределения Максвелла, можно графически определить число молекул, обладающих скоростями лежащими в заданном интервале между 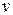 и
и 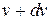 . Это число, очевидно, равно площади заштрихованной полосы с основанием
. Это число, очевидно, равно площади заштрихованной полосы с основанием 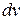 и высотой
и высотой 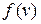 .
.
На рис.7.2 представлены также функции распределения для различных температур Т1<Т2<Т3. Видно, что с ростом Т скорости молекул возрастают и вся кривая смещается в сторону больших скоростей. При этом площади, ограниченные этими кривыми и осью абсцисс, пропорциональны общему числу частиц в единице объема и поэтому не могут изменяться с изменением температуры. Вследствие этого максимумы кривых по мере повышения температуры уменьшаются. Пользуясь формулой распределения Максвелла, можно вычислить среднеарифметическое значение скорости молекул. По определению среднеарифметическая скорость равна отношению суммы скоростей всех молекул к их общему числу
 . (7.8)
. (7.8)
Среднеквадратичная скорость
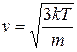 . (7.9)
. (7.9)
8. РАСПРЕДЕЛЕНИЕ МОЛЕКУЛ ПО ВЫСОТЕ В ПОЛЕ ТЯЖЕСТИ.
БАРОМЕТРИЧЕСКАЯ ФОРМУЛА.
При равновесном состоянии газа его молекулы имеют максвелловское распределение по скоростям. Далее рассмотрим, каково распределение молекул в пространстве (в объеме).
Хаотическое движение молекул приводит к тому, что частицы газа равномерно заполняют весь объем сосуда, в которой они заключены, т.е. в каждой единице объема имеется одинаковое число частиц. Но это справедливо только в том случае, когда на молекулы не действуют внешние силы. При наличии внешних сил молекулярные движения описываются другими закономерностями. В качестве примера рассмотрим газ, находящийся под действием силы тяжести (земную атмосферу). Если бы отсутствовало тепловое движение молекул, то все они под действием силы тяжести "упали" бы на землю и весь воздух тончайшим слоем собрался бы у поверхности Земли. Если бы отсутствовала сила тяжести, но существовало бы молекулярное движение, то молекулы разместились бы по всему мировому пространству. Воздушная оболочка Земли обязана своим существованием в ее теперешнем виде наличию одновременно и теплового движения молекул и силы притяжения Земли. При этом в атмосфере устанавливается вполне определенное распределение молекул по высоте. Соответственно этому распределению молекул устанавливается и определенный закон изменения давления газа с высотой. Найдем этот закон изменения давления.
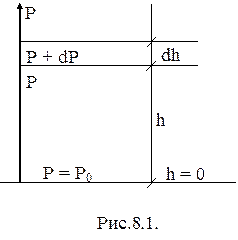
|
Рассмотрим вертикальный столб воздуха с площадью основания, равной единице (рис.8.1). Пусть у поверхности Земли, где n =0, давление равно p0, а на высоте  давление - p. При изменении высоты на dh давление изменяется на dp. Согласно закону Паскаля разность давлений p-(p+dp) равна весу газа, заключенного в объеме столба высотой dh. Вес газа
давление - p. При изменении высоты на dh давление изменяется на dp. Согласно закону Паскаля разность давлений p-(p+dp) равна весу газа, заключенного в объеме столба высотой dh. Вес газа
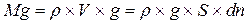 , (8.1)
, (8.1)
где  плотность газа, равная
плотность газа, равная 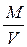 .
.
Таким образом:
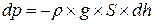 , (8.2)
, (8.2)
т.к. 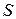 единичная площадь:
единичная площадь:
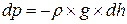 . (8.3)
. (8.3)
Согласно уравнению состояния
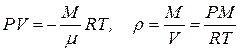 , (8.4)
, (8.4)
следовательно:
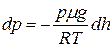 или
или 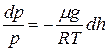 . (8.5)
. (8.5)
В общем случае Т меняется с высотой  . А для случая, когда температура с высотой не изменяется, логарифмирование дает
. А для случая, когда температура с высотой не изменяется, логарифмирование дает
 . (8.6)
. (8.6)
Потенцируя полученное выражение, находим
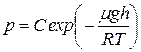 . (8.7)
. (8.7)
 Используя начальное условие p = p0 при h = 0, находим
Используя начальное условие p = p0 при h = 0, находим
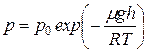 . (8.8)
. (8.8)
Эта формула называется барометрической формулой. Из нее следует, что давление убывает с высотой тем быстрее, чем тяжелее газ (чем больше 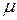 ) и чем ниже температура.
) и чем ниже температура.
9. РАСПРЕДЕЛЕНИЕ БОЛЬЦМАНА
Заменив в барометрической формуле p через  , получаем закон изменения с высотой числа частиц в единице объема:
, получаем закон изменения с высотой числа частиц в единице объема:
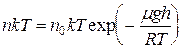 . (9.1)
. (9.1)
Здесь  - число молекул в единице объема на высоте, равной нулю,
- число молекул в единице объема на высоте, равной нулю, 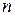 - то же число на высоте
- то же число на высоте  . Если в последнем выражении
. Если в последнем выражении 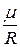 заменить равным ему отношением
заменить равным ему отношением 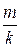 , где
, где  - масса одной молекулы,
- масса одной молекулы, 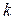 - постоянная Больцмана, то получаем
- постоянная Больцмана, то получаем
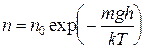 . (9.2)
. (9.2)
В полученной формуле  - представляет потенциальную энергию молекулы:
- представляет потенциальную энергию молекулы:
 . (9.3)
. (9.3)
Отсюда
 . (9.4)
. (9.4)
Формула представляет распределение молекул по значениям потенциальной энергии.
Здесь  - число молекул в единице объеме, где
- число молекул в единице объеме, где 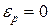 ;
;
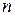 - число молекул в единице объема, в тех точках пространства, где потенциальная энергия молекул равна
- число молекул в единице объема, в тех точках пространства, где потенциальная энергия молекул равна  .
.
Больцман доказал, что эта формула справедлива для любых частиц и для любого потенциального поля. Это распределение называется распределением Больцмана.
10. ДЛИНА СВОБОДНОГО ПРОБЕГА МОЛЕКУЛ.
Теоретические расчеты и специально проведенные опыты показывают, что средняя скорость теплового движения молекул 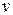 измеряется сотнями метров в секунду. Так, например, средняя скорость движения молекул воздуха в нормальных условиях равна 500 м/с. Однако если в одном конце помещения пролили каплю сильно пахнущего вещества, то его запах в другом конце комнаты вы почувствуете не сразу, а через некоторое время. Казалось бы, запах должен стать заметным сразу во всей комнате, т. к. молекулам вещества требуются лишь доли секунды, чтобы пролететь путь, равный размерам комнаты.
измеряется сотнями метров в секунду. Так, например, средняя скорость движения молекул воздуха в нормальных условиях равна 500 м/с. Однако если в одном конце помещения пролили каплю сильно пахнущего вещества, то его запах в другом конце комнаты вы почувствуете не сразу, а через некоторое время. Казалось бы, запах должен стать заметным сразу во всей комнате, т. к. молекулам вещества требуются лишь доли секунды, чтобы пролететь путь, равный размерам комнаты.
Это кажущееся противоречие объясняется тем, что каждая молекула при своем движении претерпевает очень большое число соударений с другими молекулами, и, таким образом, молекулы как бы "толкутся" на месте. Несмотря на большую скорость, молекула за 1 секунду уходит лишь на небольшое расстояние от того места, где она находилась. От столкновения до столкновения молекулы движутся прямолинейно и равномерно, проходя при этом некоторое расстояние 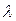 . В результате траектория молекул приобретает характерный вид ломаной линии. Прямолинейный участок траектории
. В результате траектория молекул приобретает характерный вид ломаной линии. Прямолинейный участок траектории  проходимый молекулой между двумя последовательными соударениями, называется длиной свободного пробега молекул. Величины
проходимый молекулой между двумя последовательными соударениями, называется длиной свободного пробега молекул. Величины  различны, но благодаря большому числу молекул и беспорядочности их движения можно говорить о средней длине свободного пробега молекул
различны, но благодаря большому числу молекул и беспорядочности их движения можно говорить о средней длине свободного пробега молекул 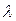 .
.
Очевидно, что
 , (10.1)
, (10.1)
где  - число соударений.
- число соударений.
Число свободных пробегов за какой-нибудь промежуток времени совпадает с числом соударений молекулы за то же время.
Если за 1 секунду молекула испытала z соударений, то длина ее траектории, численно равная средней скорости ее движения, будет состоять из z свободных пробегов. Для различных молекул это число будет различным, однако можно ввести понятие о среднем числе соударений z. Оно будет равно отношению средней скорости движения молекул к средней длине свободного пробега молекул:
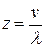 . (10.2)
. (10.2)
В дальнейшем мы увидим, что все реальные свойства газов в основном зависят от процессов соударений молекул друг с другом. Эти связанные между собой величины - средняя длина свободного пробега 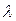 и среднее число столкновений в единицу времени
и среднее число столкновений в единицу времени 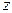 - являются основными величинами, характеризующими этот процесс. Как видно среднюю длину свободного пробега можно найти, если известно число
- являются основными величинами, характеризующими этот процесс. Как видно среднюю длину свободного пробега можно найти, если известно число 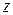 :
:
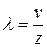 . (10.3)
. (10.3)
Среднее число столкновений z можно вычислить из следующих очень простых соображений. Молекулы будем считать твердыми упругими шариками радиусом r. Рассмотрим некоторую определенную молекулу, которая движется со скоростью 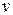 . После каждого столкновения молекула меняет направление скорости, однако для простоты предположим, что молекула и после столкновения продолжает двигаться в том же направлении, в каком она двигалась до столкновения. Кроме того, также для простоты положим, что все другие молекулы, кроме рассматриваемой, неподвижны. Тогда наша единственная движущаяся молекула, пройдя за 1 секунду расстояние, равное ее средней скорости
. После каждого столкновения молекула меняет направление скорости, однако для простоты предположим, что молекула и после столкновения продолжает двигаться в том же направлении, в каком она двигалась до столкновения. Кроме того, также для простоты положим, что все другие молекулы, кроме рассматриваемой, неподвижны. Тогда наша единственная движущаяся молекула, пройдя за 1 секунду расстояние, равное ее средней скорости 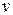 , сталкивается со всеми молекулами, которые окажутся на ее пути. Это будут те молекулы, центры которых расположены в объеме цилиндра с длиной
, сталкивается со всеми молекулами, которые окажутся на ее пути. Это будут те молекулы, центры которых расположены в объеме цилиндра с длиной 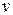 и площадью основания
и площадью основания 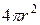 , т.к. радиус этого цилиндра равен диаметру молекулы (рис.10.1).
, т.к. радиус этого цилиндра равен диаметру молекулы (рис.10.1).

Величина  - называется эффективным сечением молекулы. Величина
- называется эффективным сечением молекулы. Величина 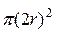 - эффективное сечение столкновения и обозначается через s,
- эффективное сечение столкновения и обозначается через s,  . Объем этого цилиндра -
. Объем этого цилиндра - 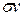 , а число молекул в нем
, а число молекул в нем 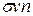 , где
, где 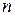 - число молекул в единице объема. Таким же будет и число столкновений z, которое испытывает выделенная нами молекула:
- число молекул в единице объема. Таким же будет и число столкновений z, которое испытывает выделенная нами молекула:
 . (10.4)
. (10.4)
Конечно, молекула не может двигаться прямолинейно, т.к. она сталкивается с другими молекулами. На самом деле путь, проходимый молекулой, зигзагообразный. Это, однако, не изменяет результатов расчета. Полагая, что молекула движется по прямой, мы только мысленно "выпрямляем" ломаный цилиндр.
Кроме того, следует еще учесть, что движется не одна, а все молекулы газа. Это значит, что в последнюю формулу должна входить не средняя скорость молекул относительно стенок сосуда, а ее скорость относительно тех молекул, с которыми она сталкивается: 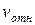 .
.
Газокинетическая теория доказывает, что эти скорости связаны между собой соотношением
 . (10.5)
. (10.5)
С учетом этого для среднего числа столкновений молекулы в единицу времени получим:
 или
или 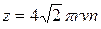 . (10.6)
. (10.6)
Средняя длина свободного пробега
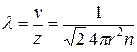 . (10.7)
. (10.7)
11. ЯВЛЕНИЯ ПЕРЕНОСА В ГАЗАХ.
Представление о средней длине свободного пробега молекул играет большую роль при объяснении механизма многих физических явлений. Это положение особенно важно при раскрытии сущности таких явлений, как внутреннее трение в газах, или вязкость, теплопроводность и диффузия газов. Все эти три явления связаны с переносом некоторой физической величины. В случае диффузии такой величиной является масса молекул, в случае вязкости это количество движения, а в случае теплопроводности - кинетическая энергия молекул газа.
Из-за того, что в основе всех этих явлений лежит одинаковый молекулярный механизм, их объединяют в одну группу, называя явлением переноса.
12. ДИФФУЗИЯ.
Диффузия - это самопроизвольное (естественное) взаимное проникновение и перемешивание частиц соприкасающихся газов, жидкостей и твердых тел. В случае газов причиной диффузии является различие концентрации в различных частях объема. Процесс перемешивания происходит до тех пор, пока концентрация молекул не становится постоянной в любой точке объема.
В результате диффузии некоторая масса газа 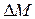 переносится из области с высокой концентрацией молекул газа в область с меньшей концентрацией.
переносится из области с высокой концентрацией молекул газа в область с меньшей концентрацией.
Экспериментально установлено, что 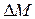 пропорциональна градиенту плотности
пропорциональна градиенту плотности 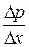 и величине площадки
и величине площадки  , установленной перпендикулярно к оси ОХ:
, установленной перпендикулярно к оси ОХ:
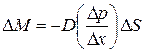 . (12.1)
. (12.1)
Величина D, зависящая от сорта газа, и от условий, при которых он находится, называется коэффициентом диффузии. Знак “минус” означает, что масса переносится в сторону убывания плотности.
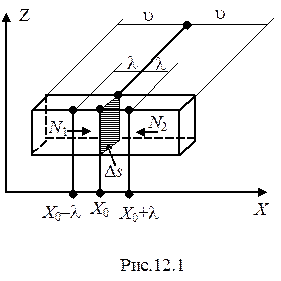
Формула характеризует явление диффузии с макроскопической точки зрения.
Рассмотрим теперь это явление с точки зрения молекулярно-кинетической теории газов. Ввиду хаотичности теплового движения молекул можно считать, что из общего числа молекул n0, заключенных в единице объема газа, 1/3 движется вдоль оси Х, 1/3 - вдоль оси Y и 1/3 - вдоль оси Z (рис.12.1). Движение молекул вдоль каждой оси в обоих направлениях равновероятно. Поэтому в положительном направлении оси Х движется 1/6 часть общего числа молекул. Будем полагать, что все молекулы обладают одной и той же скоростью теплового движения, равной средней скорости v.
Если бы плотность газа r была постоянна по всему объему, то через площадь DS за единицу времени проходило бы слева направо и справа налево одинаковое число частиц. Их количество равняется количеству частиц, находящихся в столбе газа длиной v и площадью основания DS, которое равняется 1/6 части произведения объема этого столба на число частиц в единице объема в том месте, где находится площадка DS: т.е. 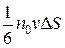 .
.
Однако мы рассматриваем простейший случай, когда  . Поскольку
. Поскольку 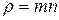 , а
, а  , то и n зависит от Х:
, то и n зависит от Х:  . Поскольку за единицу времени через поверхность
. Поскольку за единицу времени через поверхность  слева направо и справа налево проходит разное число молекул, т.е. в газе имеет место перетекание молекул в одном направлении, а, следовательно, перенос их массы.
слева направо и справа налево проходит разное число молекул, т.е. в газе имеет место перетекание молекул в одном направлении, а, следовательно, перенос их массы.
Пусть  уменьшается с ростом координаты Х, т.е. перетекание массы происходит слева направо. Число молекул, проходящих через
уменьшается с ростом координаты Х, т.е. перетекание массы происходит слева направо. Число молекул, проходящих через  слева направо -
слева направо -  , а справа налево -
, а справа налево - 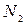 .
.
На пути свободного пробега не изменяются ни величина, ни направление скорости молекул. Поэтому в среднем можно считать, что поверхности  беспрепятственно достигают только 1/6 часть всех молекул, отстоящих от нее по обе стороны на расстоянии средней длины свободного пробега
беспрепятственно достигают только 1/6 часть всех молекул, отстоящих от нее по обе стороны на расстоянии средней длины свободного пробега 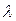 .
.
Тогда
 ; (12.2)
; (12.2)
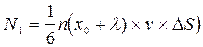 ,
,
где  и
и 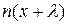 - число частиц в единицах объемов, соответствующих координатам
- число частиц в единицах объемов, соответствующих координатам 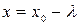 и
и 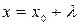 . Тогда число частиц, проходящих через
. Тогда число частиц, проходящих через  в положительном направлении оси Х
в положительном направлении оси Х
 . (12.3)
. (12.3)
Умножая это равенство на массу молекулы, получаем выражение для массы вещества 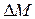 , прошедшего за единицу времени через площадку
, прошедшего за единицу времени через площадку  в направлении оси Х:
в направлении оси Х:
 . (12.4)
. (12.4)
Из математического анализа (теорема Лагранжа), известно, что
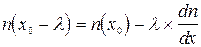 , (12.5)
, (12.5)
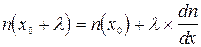 .
.
Из этих математических выражений следует
 , (12.6)
, (12.6)
где величина 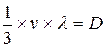 - называется коэффициентом диффузии.
- называется коэффициентом диффузии.
13. ВЯЗКОСТЬ.
Пусть вдоль цилиндрического канала радиуса R происходит спокойное, монотонное течение газа или жидкости со скоростью U.
Эксперименты показывают, что наибольшая скорость течения наблюдается на оси канала и по мере приближения к стенкам скорость U уменьшается, а слой непосредственно у стенки находится в состоянии покоя, т.е. U=f(R).
Для наглядности мысленно поток разделим на несколько слоев и плавное изменение скорости U заменим ступенчатой, приближенной линией (рис.13.1). Теперь явно видно изменение скорости от одного слоя к другому. Чтобы понять

происхождение силы внутреннего трения, рассмотрим движение молекул в двух соседних слоях газа.
В каждом слое любая молекула газа участвует в двух движениях: тепловом, со средней скоростью 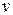 , и направленном вдоль канала или переносном, со скоростями
, и направленном вдоль канала или переносном, со скоростями  ,.... Тепловое движение хаотическое, поэтому молекулы непрерывно переходят из одного слоя в другой. Например, через контрольную площадку S за время
,.... Тепловое движение хаотическое, поэтому молекулы непрерывно переходят из одного слоя в другой. Например, через контрольную площадку S за время 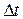 проходят вверх и вниз потоки молекул:
проходят вверх и вниз потоки молекул:
 ,
,  . (13.1)
. (13.1)
Поскольку давление и температура во всем объеме газа одинаковы, то 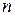 и
и 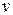 - постоянные, следовательно,
- постоянные, следовательно, 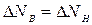 . Однако верхние молекулы обладают количеством движения
. Однако верхние молекулы обладают количеством движения 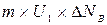 и переносят его в нижний слой, а молекулы нижнего слоя переносят в верхний
и переносят его в нижний слой, а молекулы нижнего слоя переносят в верхний 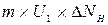 . Таким образом, происходит постоянный обмен количеством движения между слоями и в результате количество движения слоя изменяется на [
. Таким образом, происходит постоянный обмен количеством движения между слоями и в результате количество движения слоя изменяется на [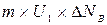 -
- 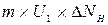 ]. Это изменение в соответствии со вторым законом динамики должно быть равно импульсу силы внутреннего трения Fтр.
]. Это изменение в соответствии со вторым законом динамики должно быть равно импульсу силы внутреннего трения Fтр.
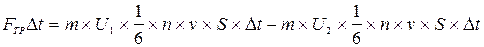 . (13.2)
. (13.2)
Сила, действующая на единицу площади границы соседних слоев
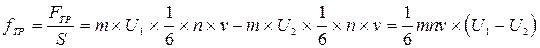 . (13.3)
. (13.3)
Из формул следует, что сила, с которой взаимодействуют два смежных слоя, равна изменению количества движения молекул за одну секунду.
Значения скоростей 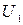 и
и  должны быть взяты непосредственно у контрольной площадки
должны быть взяты непосредственно у контрольной площадки  . Так как скорость изменяется благодаря столкновениям молекул, то толщина слоя должна быть не более
. Так как скорость изменяется благодаря столкновениям молекул, то толщина слоя должна быть не более 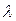 . Поэтому разность
. Поэтому разность 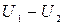 представляет собой приращение скорости
представляет собой приращение скорости 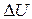 на расстоянии
на расстоянии  . Следовательно, можно составить следующее соотношение:
. Следовательно, можно составить следующее соотношение:
 . (13.4)
. (13.4)
Здесь 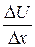 представляет собой градиент скорости поступательного движения газа:
представляет собой градиент скорости поступательного движения газа:
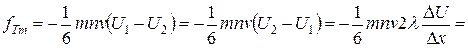
 ,
,
где 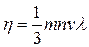 ,
, 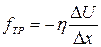 , т.е. сила внутреннего трения, возникающая при движении в газе, прямо пропорциональна градиенту скорости. Коэффициент пропорциональности
, т.е. сила внутреннего трения, возникающая при движении в газе, прямо пропорциональна градиенту скорости. Коэффициент пропорциональности  носит название коэффициента внутреннего трения или просто вязкости газа. Вязкость
носит название коэффициента внутреннего трения или просто вязкости газа. Вязкость  численно равна силе внутреннего трения, действующей на единицу площади границы движущихся слоев газа, когда скорость движения уменьшается на одну единицу скорости при перемещении в перпендикулярном направлении на единицу длины.
численно равна силе внутреннего трения, действующей на единицу площади границы движущихся слоев газа, когда скорость движения уменьшается на одну единицу скорости при перемещении в перпендикулярном направлении на единицу длины.
Этот закон впервые был получен Ньютоном и является основным при изучении движения вязкой жидкости и газа. Этим же законом определяется сила трения, возникающая на границе между газом и движущейся в этом газе твердым телом.
14. ТЕПЛОПРОВОДНОСТЬ.
Если в вещественной среде вдоль произвольного направления Х температура не остается постоянной, то вдоль этого направления возникает поток тепла. Это явление возникновения потока тепла называется теплопроводностью. Таким образом, в процессе теплопроводности происходит перенос энергии от более нагретых областей к менее нагретым. Этот перенос осуществляется благодаря тепловому, хаотическому движению молекул, или перемешиванию молекул, имеющих различные энергии.
Рассмотрим случай, когда верхняя стенка объема с газом нагревается, а нижняя остается при комнатной температуре. Это значит, что вдоль вертикального направления температура газа не остается постоянной. В результате образуется поток тепла сверху вниз (рис.14.1)
Результирующий поток тепла свер
|
|
|
|
|
Дата добавления: 2014-01-11; Просмотров: 1627; Нарушение авторских прав?; Мы поможем в написании вашей работы!