Представления конечных автоматов

Автомат может быть задан различными способами, например, путем словесного описания его функционирования или перечислением элементов множеств X, Y, S, с указанием отношений между ними. При анализе и син­тезе конечных автоматов используются стандартные формы пред­ставления: таблицы, графы и матрицы. Элементы множеств X, Y, S удобно пронумеровать порядковыми числами, начиная с нуля, например: Х = {0, 1, 2, 3},
Y = {0, 1, 2, 3} и S = {0, 1, 2, 3}. Тогда характеристические функции d и l можно представить двумя таблицами, строки которых соответствуют состояниям, а столбцы - входам. Первая таблица, называемая таблицей переходов, соответ­ствует функции 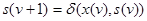, и ее клетки заполняются номерами состояний s (v +1), в которые переходит автомат при воздействии x(v), и состоянии s(v) в данный тактовый момент. Вто­рая таблица, называемая таблицей выходов, соответствует функции 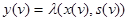, и ее клетки заполняются номерами выходов y(v) в данный тактовый момент, которые соответствуют воздействию x(v) и состоянию s(v) в тот же момент. Например, для заданных множеств X, Y, S такие таблицы могут иметь вид:

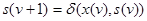
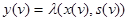
x(v) s(v)					x(v) s(v)

Обе таблицы можно объединить в общую таблицу переходов, если условиться записывать в клетках пары чисел (номер следую­щего состояния в числителе и номер выхода в знаменателе), т. е.

x(v) s(v)
	3/0	2/0	1/0	3/0
	3/1	2/0	1/0	3/1
	3/1	2/0	2/1	3/1
	3/0	0/0	0/1	1/1

Граф автомата строится таким образом, что его вершины соот­ветствуют состояниям, а направленные дуги обозначаются как дизъюнкции входов, под воздействием которых совершается пере­ход из одного состояния в другое по направлению дуги. В знамена­телях записываются номера выходов, соответствующие этим пере­ходам.

Пример. На рис. 11.2 показан граф, построенный в соответствии с при­веденной выше общей таблицей переходов. Так как из состояния 0 автомат переходит в состояния 1, 2 и 3, то из вершины 0 графа исходят дуги в вершины 1, 2 и 3. При этом переход в состояние 1 совершается под воздействием 2 и ему соответствует выход 0, поэтому дуга из вершины 0 в 1 помечается как 2/0. Переход в состояние 2 совершается под воздействием 1 и ему соответствует выход 0, поэтому дуга из вершины 0 в 2 помечается как 1/0. Переходы в со­стояние 3 совершаются под воздействиями 0 и 3, и им обоим соответствует выход 0, поэтому дуга из вершины 0 в 3 помечается как дизъюнкция 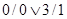. Аналогично определяются и другие дуги графа. Петли соответствуют переходам, при которых состояния не изменяются. Так, рассматриваемый автомат переходит из состояния 2 в 2 под воздействиями 1 и 2, которым соответствуют выходы 0 и 1. Следовательно, петля при вершине 2 помечается как дизъюнкция 1/0Ú2/1.

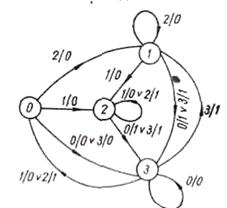Рис.11.2. Граф конечного автомата

Матрица соединения автомата М (или матрица переходов) представ­ляет собой квадратную таблицу, в ко­торой номера строк и столбцов соот­ветствуют номерам состояний. Клетка матрицы на пересечении i -й строки и j -го столбца заполняется дизъюнкцией пар «вход-выход», которая приписана дуге графа исходящей из i -й в j -ю вершину. При отсутствии такой ветви клерка заполняется нулем или остается свободной. Так для рассматриваемого примера имеем:

М =		2/0	1/0	0/0Ú3/0
	2/0	1/0	0/1Ú3/1
		1/0Ú2/1	0/1Ú3/1
1/0Ú2/1	3/1		0/0

Дата добавления: 2014-01-13