Лекція 11. Ця задача відіграла значну роль у розвитку теорії лінійного програмування, і тому їй приділяється велика увага

Транспортна задача

Ця задача відіграла значну роль у розвитку теорії лінійного програмування, і тому їй приділяється велика увага. Крім того, до цієї задачі зводиться широкий клас практичних задач, зокрема задач автоматизованого проектування. Розглянемо неформальну постановку задачі.

Нехай є m пунктів постачання (постачальників) однородного продукту з запасами b₁, b₂,…,b_m; b_i – запас продукту у і-го постачальника. Крім того, є n пунктів споживання (споживачів) з потребами p₁, p₂,…,p_n; p_j – потреби продукту j-го споживача. Відомі також ціни перевезення продукту (вартості перевезення одиниці продукту) від кожного постачальника до кожного споживача; с_ij – ціна перевезення продукту від і-го постачальника до j-го споживача

С= || с_ij ||^m,n_i,j=1.

Треба скласти план перевезеня продукту таким чином, щоб врахувати запаси постачальників, потреби споживачів і забезпечити мінімальні сумарні витрати на перевезення.

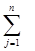
Розглянемо окремий випадок транспортної задачі, коли сумарні потреби споживачів дорівнюють сумарним запасам постачальників.

b_i = p_j. (11.1)

Задача, для якої виконується умова (11.1) називається збалансованою транспортною задачею або транспортною задачею закритого типу. Розв’язком такої задачі є план, згідно з яким уся продукція від постачальників перевозиться до споживачів.

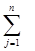
Побудуємо математичну модель збалансованої транспортної задачі. Позначимо через x_ij – шуканий об’єм перевезення від і-го постачальника до j-го споживача (i = 1, m; j = 1, n). Тоді цільова функція приймає вигляд

F = c_ij x_ij ® min.

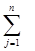
Подані запаси продуктів можна врахувати за допомогою системи рівнянь

x_ij = b_i, i = 1, m.

Ліва частина кожного рівняння цієї системи складає сумарний об’єм продукту, вивезеного від відповідного постачальника.

Дата добавления: 2014-01-13