Потреби споживачів враховуються системою рівнянь

x_ij = p_j, j = 1, n,

у якій ліва частина кожного j-го рівняння дорівнює сумарному об’єму продукту, перевезеного до i-го споживача.

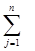Враховуючи, що об’єми перевезень повинні бути невід’ємні, остаточно отримуємо математичну модель у вигляді

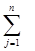F = c_ij x_ij ® min, (11.2)

x_ij = b_i, i = 1, m, (11.3)

x_ij = p_j, j = 1, n, (11.4)

x_ij ³ 0, i = 1, m, j = 1, n. (11.5)

Як бачимо, подана задача є задачею лінійного програмування у канонічній формі. Проаналізуємо отриману задачу, а саме матрицю A коефіцієнтів непрямих обмежень. Для цього запишемо непрямі обмеження у розгорнутому вигляді

x₁₁ + x₁₂ + … + x_1n = b₁,

x₂₁ + x₂₂ + … + x_2n = b₂,

(11.6)

x_m1 + x_m2 + … + x_mn = b_m,

x₁₁ + x₂₁ + … + x_m1 = p₁,

x₁₂ + x₂₂ + … + x_m2 = p₂,

x_1n + x_2n + … + x_mn = p_n.

Внаслідок (11.1) сума перших m рівнянь дорівнює сумі останніх n. Тому система непрямих обмежень транспортної задачі лінійно залежна. Разом з тим, якщо вилучити будь-яке одне рівняння, утворюється лінійно незалежна система.

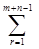Для того, щоб довести цю лінійну незалежність, треба показати, що з рівняння

k_ra^’_r, = 0, (11.7)

(де a^’_r - r-й рядок матриці A^’, отриманої з матриці A після вилучення деякого рядка; k_r – дійсний коефіцієнт)

прямує k_r = 0, r = 1, m + n – 1.

Дійсно, кожний стовпець матриці A містить два одиничних елементи і усі інші – нульові. Одна одиниця належить першій групі рівнянь (перші m рівнянь), а друга – другій (останні n). При вилученні, наприклад, q-го рівняння з першої групи стовпці, що містили одиницю у вилученому рядку, будуть містити тільки один ненульовий елемент. Оскільки ці елементи розташовані по одному у кожному з рядків другої групи з (11.7) прямує, усі коефіцієнти k_r для рядків другої групи дорівнюють нулю. А звідси прямує, що усі коефіцієнти і для рядків першої групи мають нульові значення.

Аналогічно можна показати, що при вилученні рівняння з другої групи також усі k_r мають нульові значення.

Таким чином ранг матриці A дорівнює m + n – 1, і це означає, що кожний опорний план транспортної задачі має m + n – 1 базисну змінну.

Розглянемо метод розв’язування транспортної задачі, який називається методом потенціалів. Цей метод можна вважати спеціальною реалізацією симплекс-методу, заснованою на урахуванні особливостей транспортної задачі.

Дата добавления: 2014-01-13