
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Покроковий опис методу потенціалів
|
|
|
|
Метод складається з двох етапів: визначення початкового опорного плану і поліпшення поточного опорного плану.
Перший етап являє собою ітераційну процедуру визначення базисних змінних опорного плану. На кожній ітерації виконуються такі кроки.
1. У невикресленій частині транспортної матриці вибирати клітинку (i, j) (ця клітинка відповідає базисній змінній xij і називається базисною) і покласти xij = min {bi,pj }.
2. У випадку, коли bi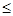 pj, потреби j-го споживача зменшити: p’j = pj - xij, а і-й рядок транспортної матриці викреслити.
pj, потреби j-го споживача зменшити: p’j = pj - xij, а і-й рядок транспортної матриці викреслити.
3. У випадку, коли bi > pj, запаси і-го постачальника зменшити: b’i = bi - xij, а j-й стовпчик транспортної матриці викреслити.
Ітерації повторюються, доки транспортна матриця містить невикреслені елементи.
Другий етап являє собою ітераційну процедуру покращення поточного опорного плану. На кожній ітерації виконуються такі кроки.
1. Визначити потенціали ui (i = 1, m), vj (j = 1, n) (аналоги симплекс-множників) для поточної транспортної матриці. Для цього скласти систему рівняннь, у якій кожне рівняння відповідає окремій базисній змінній. Змінній xij відповідає рівняння cij + ui + vj = 0.
2. Приcвоїти довільному потенціалу нульове значення і визначити з отриманої системи усі інші потенціали.
3. Визначити у транспортній матриці небазисну клітинку (i, j), для якої cij + ui + vj < 0. Якщо така клітинка не існує, поточна транспортна матриця оптимальна – кінець алгоритму.
4. Починаючи з визначеної клітинки, побудувати у транспортній матриці цикл, що містить, крім клітинки (i, j), тільки базисні клітинки. Сусідні клітинки циклу повинні бути розташовані у одному стовпчику або у одному рядку.
5. Пронумерувати клітинки циклу за порядком обходу, присвоївши клітинці (i, j) номер 1. Серед клітинок з парними номерами визначити ту, нехай (r, s), якій відповідає мінімальний об’єм перевезення.
6. Для клітинок циклу з непарними номерами збільшити об’єми перевезень на величину xrs, а для клітинок з парними - зменшити на xrs. Після цього клітинка (r, s) стає небазисною, а (i, j) – базисною.
 Незбалансована транспортна задача
Незбалансована транспортна задача
У незбалансованій задачі bi 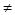 pj. Така задача розв’язується шляхом зведення до збалансованої. Відрізняють два випадки.
pj. Така задача розв’язується шляхом зведення до збалансованої. Відрізняють два випадки.
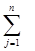
 Перший випадок - сума запасів перебільшує суму потреб:
Перший випадок - сума запасів перебільшує суму потреб:
bi > pj,

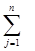


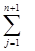 тобто увесь продукт перевезти від постачальників до споживачів не можливо, і частина продукту залишається у постачальників. Для приведення вихідної задачі до збалансованої уводиться фіктивний споживач, потреби pn+1, якого визначаються таким чином pn+1 = bi - pj. Ціни ci n+1 (i = 1, m) на перевезення товару до фіктивного споживача визначаються як штрафи за зберігання одиниці продукту у i-го постачальника. У результаті отримуємо збалансовану транспортну задачу.
тобто увесь продукт перевезти від постачальників до споживачів не можливо, і частина продукту залишається у постачальників. Для приведення вихідної задачі до збалансованої уводиться фіктивний споживач, потреби pn+1, якого визначаються таким чином pn+1 = bi - pj. Ціни ci n+1 (i = 1, m) на перевезення товару до фіктивного споживача визначаються як штрафи за зберігання одиниці продукту у i-го постачальника. У результаті отримуємо збалансовану транспортну задачу.
 F = cij xij
F = cij xij 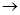 min,
min,

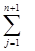
 xij = pj, j = 1, n+1,
xij = pj, j = 1, n+1,

 xij = bi, i = 1, m,
xij = bi, i = 1, m,
xij 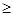 0, i = 1, m, j = 1, n+1.
0, i = 1, m, j = 1, n+1.
Якщо треба, щоб від деяких постачальників продукція обов’язково була вивезена, приймають, що штрафи за зберігання продукції у таких постачальників дорівнюють великому абстрактному числу M, що більше будь-якого конкретного. Зрузуміло, що сумарні запаси таких постачальників не повинні перебільшувати сумарних потреб реальних споживачів.
Якщо за зберігання продукції у деякого постачальника не треба сплачувати ніяких штрафів, то штрафу для цього постачальника присвоюють нульове значення.

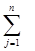 Другий випадок – сума потреб перебільшує суму запасів:
Другий випадок – сума потреб перебільшує суму запасів:
bi < pj,
тобто задовольнити потреби усіх споживачів не можливо, і для частини з них при будь-якому плані має місце недопостачання. Для приведення цієї задачі до збалансованої уводять фіктивного постачальника, запаси bm+1, якого визначаються таким чином bm+1 = pj - bi. Ціни cm+1j (j = 1, n) на перевезення товару від фіктивного постачальника визначаються як штрафи за недопостачання одиниці продукту j-му споживачу. У результаті отримуємо збалансовану транспортну задачу.

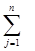
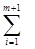

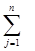

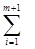 F = cij xij
F = cij xij 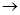 min,
min,

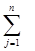 xij = pj, j = 1, n,
xij = pj, j = 1, n,
xij = bi, i = 1, m + 1,

 xij
xij 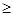 0, i = 1, m+1, j = 1, n.
0, i = 1, m+1, j = 1, n.
Якщо треба, щоб до деяких споживачів продукція обов’язково була перевезена, приймають, що штрафи за недопостачання продукції до таких споживачів дорівнюють великому абстрактному числу M, що більше будь-якого конкретного. Зрузуміло, що сумарні потреби таких споживачів не повинні перебільшувати сумарних запасів реальних постачальників.
Якщо за недопостачання продукції до деякого споживача не треба сплачувати ніяких штрафів, то штрафу для цього споживача присвоюють нульове значення.
|
|
|
|
|
Дата добавления: 2014-01-13; Просмотров: 434; Нарушение авторских прав?; Мы поможем в написании вашей работы!