Поняття дробу. Рівність дробів

Раціональні числа

Виникнення дробів було обумовлено вимірюванням величин. Покажемо необхідність виникнення дробів при вимірюванні, наприклад, довжини відрізка.

Нехай дані одиничний відрізок е і а. Якщо існує натуральне число q таке, що а =qе, то m(a) = q (m(a)– довжина відрізка а при одиничному відрізку е).

Відрізок а довший ніж 4е, але коротший ніж 5е. Тому його довжину при одиничному відрізку е не можна виразити натуральним числом.

Означення 10. Нехай дано одиничний відрізок е і відрізок а,

причому е = nе1, n Є N, то вважають, що m(a) =

де т(а) — довжина відрізка а. Символ 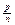, в

якому ріп — натуральні числа, називають дробом з чисельником р і зна­менником п. У цьому випадку пишуть також а = 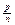eі говорять, що відрізок а сумірний з e.

При умовах цього означення очевидним є таке твердження:

т (а) = 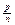na = pe

Теорема 11. Довжина одного й того самого відрізка при зада­ному одиничному відрізку може виражатися різними дробами.

Доведення. Нехай а — деякий відрізок, для якого т (а) =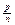

при заданому одиничному відрізку e. Тоді па = ре і для довільного натурального числа ℓ маємо (пℓ) а = (рℓ) e. Ця рівність означає, що m(a) = i інший дріб, що виражає довжину відрізка а.

Теорему доведено.

З викладеного вище випливає, що довжина будь-якого відрізка, сумірного з одиничним відрізком, виражається певним дробом. Чи кожний дріб є довжиною певного відрізка? Відповідь на це запитання дає таке

Твердження: для будь-якого дробу існує відрізок, довжина якого виражається цим дробом.

Теорема 12. Для того щоб дроби 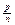і виражали довжи-

ну одного й того самого відрізка, необхідно й достатньо, щоб викону­валася рівність рk = пq.

Означення 11. Дроби 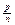і називають рівними якщо рк = пq.

На основі сказаного вище виконується таке

твердження: два дроби рівні тоді і тільки тоді, коли вони виражають довжину одного й того самого відрізка.

Теорема 13 (основна властивість дробу). Якщо чисельник і зна­менник дробу помножити на довільне натуральне число або розділити на довільний їхній спільний дільник, то дістанемо дріб, що дорівнює даному.

На цій властивості грунтується скорочення дробів і зведення дробів до спільного знаменника.

Скорочення дробів — це заміна даного дробу іншим, що дорівнює даному, але з меншими чисельником і знаменником.

Якщо треба дістати дріб, що дорівнює даному з якомога меншими чисельником і знаменником, то, очевидно, треба поділити чисельник і знаменник на їхній НСД.

Дріб, у якого чисельник і внаменник взаємно прості, називають

нескоротним.

Зведення дробу до спільного знаменника – це заміна даних дробів дробами, що дорівнюють їм, і мають однакові знаменники. Нехай задано дроби 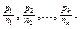Позначимо через n – довільне спільне кратне знаменників n₁, n₂, …, n_k. Тоді n = n₁t₁ = n₁t₁ = n₂t₂ = … = n_kt_k. Помноживши чисельники і знаменники даних дробів відповідно на t₁, t₂, …, t_k, дістанемо

,

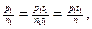
Тобто дані дроби замінили дробами, кожний з яких має знаменником число n. Це число називають спільним знаменником даних дробів. Часто намагаються дістати найменший спільний знаменник, ним, очевидно, буде НСК знаменників даних дробів.

Дата добавления: 2014-01-13