Графічне розв’язування ігор

Використання критерію максиміну відповідає вибору гравцем 1 таких xi, при яких максимізується найменший очікуваний виграш при виборі гравцем 2 довільної дії. Аналогічно, застосування мінімаксного критерію для гравця 2 означає визначення таких yj, при яких мінімізується найбільший очікуваний програш при виборі гравцем 1 довільної дії. Таким чином, критерій визначення стратегії гравця 1 має вигляд

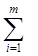
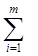max{min{ a_ij x_i | j = 1, n}| 0 £ x_i £ 1, i = 1, m & x_i = 1 },

а стратегії гравця 2 -

min{max{ a_ij y_j | i = 1, m}| 0 £ y_j £ 1, j = 1, n & y_j = 1 }.

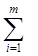
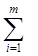Для кожної конкретної стратегії гравця 1 x⁰ = (x⁰₁, x⁰₂, …, x⁰_m) величина min{ a_ij x⁰_i | j = 1, n} являє собою мінімальне очікуване значення виграшу, яке називають очікуваним максимінним значенням, а для кожної конкретної стратегії гравця 2 y⁰ = (y⁰₁, y⁰₂, …, y⁰_n) величина max { a_ij y⁰_j | i = 1, m } є максимальним очікуваним значенням програшу, яке називають очікуваним мінімаксним значенням. Кожній парі стратегій (x⁰, y⁰) відповідає очікуване значення виграшу гравця 1, або програшу гравця 2, що визначається виразом

T⁰ = a_ij x⁰_i y⁰_j,

оскільки вибори дій гравцями 1 та 2 можна розглядати як незалежні випадкові події, і тоді x⁰_i y⁰_j є ймовірністю події, у якій значення виграшу (програшу) дорівнює a_ij.

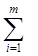
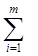
Якщо отримані в результаті розв’язання задачі значення ймовірностей позначити як x^* = (x^*₁, x^*₂, …, x^*_m) та y^* = (y^*₁, y^*₂, …, y^*_n), то згідно з відомою теоремою про мінімакс

T^* = a_ij x^*_i y^*_j = min{ a_ij x^*_i | j = 1, n} = max{ a_ij y^*_j | i = 1, m },

тобто для будь-якої матричної гри для оптимальних стратегій очікуване мінімаксне значення дорівнює очікуваному максимінному значенню і дорівнює очікуваному значенню виграшу гравця 1 (програшу гравця 2). Доведення цієї теореми розглянемо пізніше.

У випадку, коли для одного з гравців визначені лише дві можливі дії, матрична гра може бути розв’язана графічним методом. Припустимо, гравець 1 має тільки дві можливі дії. Тоді стратегія цього гравця визначається тільки одним числом x₁, оскільки x₂ = 1 - x₁. Очікуваний виграш гравця 1 при j-й дії гравця 2 являє собою лінійну функцію x₁: a_1jx₁ + a_2j x₂ = a_1j x₁ + a_2j (1 – x₁) = (a_1j - a_2j) x₁ + a_2j. Тому пошук оптимальної стратегії гравця 1 зводиться до побудови прямих залежності очікуваного виграшу цього гравця від x₁, визначенню ламаної залежності мінімального (по усіх можливих діях гравця 2) очікуваного виграшу гравця 1 від x₁, і наступного визначення на побудованій ламаній точки з максимальною ординатою. Після того, як знайдено оптимальну стратегію для гравця 1 оптимальну стратегію для гравця 2 можна визначити, припустивши, що гравець 2 застосовує не більше двох дій з ненульовою ймовірністю при умові, що при цьому розв’язок гри не змінюється.

Таблиця 18.2

Стратегії гравця 2
Стратегії гравця 1
				-1

Розглянемо приклад графічного розв’язування матричної гри з вихідними даними у табл.18.2.

Таблиця 18.3

Дії гравця 2	Очікуваний виграш гравця 1
	(a11 - a21) x1 + a21 = -2x1 + 4
	(a12 - a22) x1 + a22 = - x1 + 3
	(- a13 - a23) x1 + a23 = x1 + 2
	(a14 - a24) x1 + a24 = -7x1 + 6

Рівняння прямих залежності очікуваних виграшів гравця 1 від x₁ наведені у табл.18.3, а самі прямі показані на мал. 18.1, де жирною лінією виділена ламана залежності мінімального очікуваного виграшу гравця 1 від x₁. Точка з максимальною ординатою на цій ламаній має абсцису x^*₁ = 1/2, яка і визначає оптимальну стратегію гравця 1.

Для визначення оптимальної стратегії гравця 2 скористаємося тим фактом, що, як прямує з мал.18.1, розв’язок задачі не змінеться, якщо прийняти, що гравець 2 застосовує тільки дві дії 3 і 4 або 3 і 2. Зауважимо, що припустити застосування гравцем 2 тільки двох дій 2 і 4 не можна, оскільки при цьому оптимальна точка змінює своє положення та опиняється на вісі T, а гра стає стабільною.

Таблиця 18.4

Дії гравця 1	Очікуваний програш гравця 2
	(a13 - a14) y^*3 + a14 = 4y^*3 - 1
	(a23 - a24) y^*3 + a24 = -4y^*3 + 6

T

6

5

4

3

2

1 x₁

0 x^*₁ = 1/2 -1

Мал.18.1. Графічне розв’язання

матричної гри.

Нехай, гравець 2 використовує дії 3 і 4, тобто y^*₁ = y^*₂ = 0, y^*₃ = 1 - y^*₄. Очікуваний програш гравця 2 при i-й дії гравця 1 визначається виразом a_i3y^*₃ + a_i4y^*₄ = a_i3 y^*₃ + a_i4 (1 - y^*₃) = (a_i3 - a_i4)y^*₃ + a_i4. Очікувані програші гравця 2 наведені у табл.18.4. Значення y^*₃ отримуємо як координату точки перетинання прямих T = 4y^*₃ – 1 і T = -4y^*₃ + 6, тобто з рівняння 4y^*₃ – 1 = -4y^*₃ + 6. Звідси маємо y^*₃ = 7/8, а y^*₄ = 1/8. Таким чином, для гравця 1 отримуємо оптимальну стратегію x^*₁ = 1/2, x^*₂ = 1/2, а для гравця 2 - y^*₁ = 0, y^*₂ = 0, y^*₃ = 7/8, y^*₄ = 1/8. Мінімальний очікуваний виграш гравця 1 (очікуване максимінне значення) отримуємо, підставляючи x^*₁ = 1/2 у рівняння, наприклад, прямої T = - x₁ + 3, T = 2.5. Максимальний очікуваний програш гравця 2 (очікуване мінімаксне значення) отримуємо, підставляючи y^*₃ = 7/8 у рівняння T = 4y^*₃ – 1, T = 2.5, що узгоджується з теоремою про мінімакс. Обчислюючи очікуване максимінне значення за формулою

T = a_ijx^*_i y^*_j,

отримуємо

T = 2*(1/2)*0 + 2*(1/2)*0 + 3*(1/2)*(7/8) + (-1)*(1/2)*(1/8) + 4*(1/2)*0 + 3*(1/2)*0 + 2*(1/2)*(7/8) + 6*(1/2)*(1/8) = 21/16 – 1/16 + 14/16 + 6/16 = 2.5.

Дата добавления: 2014-01-13