Приклад. ні функції для роботи з векторами та матрицями

Основ

ні функції для роботи з векторами та матрицями

1 ) matrix(m,n,f) - створення та заповнення матриці розмірністю m* n, при цьому кожний елемент матриці дорівнює значенню функції f(x,y), де x - номер рядка, y - номер стовпчика.

Приклад. Створити матрицю А, що містить 3 рядка і 4 стовпчика. Елементи матриці обчислюються за формулою x+ y, де x - номер рядка, y - номер стовпчика.

Розв’язок.

2) diag(V) - створення діагональної матриці, де елементами діагоналі є елементи вектора V.

Приклад. Створити діагональну матрицю В, у якій діагональні елементи містять елементи заданого вектора V=.

Розв’язок. V= B:=diag(V)

3) identity(n) - створення одиничної матриці розмірності n* n.

Приклад. Створити одиничну матрицю розмірністю 3.

Розв’язок.

4) augment(A,B) - формує матрицю, в перших стовпцях якої розміщується матриця A, а в останніх – матриця B. При цьому обидві матриці повинні мати однакову кількість рядків.

Приклад. Створити матрицю D,в перших стовпцях якої розміщуються елементи матриці A, а в останніх – елементи матриці B.

Розв’язок.

5) stack(A,B) - формує матрицю, в перших рядках якої розміщується матриця A, а в останніх – матриця B. При цьому обидві матриці повинні мати однакову кількість стовпчиків.

Приклад. Створити матрицю F, в перших рядках якої розміщуються елементи матриці A, а в останніх – елементи матриці B.

Розв’язок.

6) submatrix(Z,r1,r2,c1,c2) - виділяє з матриці підматрицю. r1 - номер початкового рядка, r2 - номер кінцевого рядка, c1 - номер початкового стовпця, c2 - номер кінцевого стовпця.

Приклад. Виділити підматрицю Z1, що містить 0-й і 1-й рядки та 0-й і 1-й стовпчики заданої матриці Z.

Розв’язок.

За допомогою цієї функції можна виділити з матриці стовпчик, рядок та окремий елемент.

Приклад. Виділити елементи 1-го стовпчика із заданої матриці Z.

Розв’язок. Submatrix (Z,0,2,1,1)=

Приклад. Виділити елементи 2-го рядка із заданої матриці Z.

Розв’язок. Submatrix (Z,2,2,0,2)=

Приклад. Виділити із заданої матриці Z елемент, розташований на перетині 1-го рядка і 2-го стовпчика.

Розв’язок. Submatrix (Z,1,1,2,2)=3

7) last(Y) - обчислює номер останнього елемента вектора.

Приклад. Обчислити номер останнього елемента заданого вектора Y.

Розв’язок.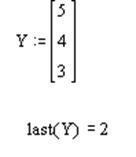

8) length(Y) - обчислює довжину вектора (кількість елементів у векторі).

Приклад. Обчислити довжину заданого вектора Y.

Розв’язок.

9) reverse(Y) - переставляє елементи вектора в оберненому порядку.

Приклад. Переставит елементи заданого вектора Y в оберненому порядку

Розв’язок. reverse(Y)=

10) cols(M) - визначає кількість стовпців у матриці.

Приклад. Визначити кількість стовпців у заданій матриці Z.

Розв’язок.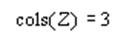

11) rows(M) - визначає кількість рядків у матриці.

Приклад. Визначити кількість рядків у заданій матриці Z.

Розв’язок.

12) max(M) - визначає найбільший елемент матриці.

Приклад. Визначити найбільший елемент заданої матриці Z.

Розв’язок.

13) min(M) - визначає найменший елемент матриці.

Приклад. Визначити найменший елемент заданої матриці Z.

Розв’язок.

14) tr(M) - обчислення сліду (суми діагональних елементів квадратної матриці)

Приклад. Обчислити слід заданої матриці М.

Розв’язок.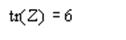

15) sort(V) - виконує сортування елементів вектора за зростанням.

Приклад. Відсортувати елементи заданого вектора Y за зростанням.

Розв’язок.

16) csort(M,i) - виконує сортування за зростанням елементів і-го стовпчика квадратної матриці за рахунок перестановки відповідних рядків.

Приклад. Відсортувати елементи 1-го стовпчика заданої матриці Z за зростанням.

Розв’язок.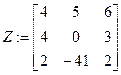

Приклад. Відсортувати елементи 1-го стовпчика заданої матриці Z за зростанням, використовуючи функцію sort.

Розв’язок.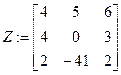

Приклад. Відсортувати задану матрицю Z по стовпчикам за зростанням елементів.

Розв’язок.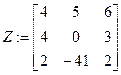

17) rsort(M,i) - виконує сортування за зростанням елементів і-го рядка квадратної матриці за рахунок перестановки відповідних стовпчиків.

Приклад. Відсортувати елементи 0-го рядка заданої матриці Z за зростанням.

Розв’язок.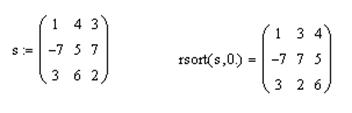

Приклад. Відсортувати всі рядки заданої матриці S за зростанням елементів. Розв’язок:

1) задати початкову матрицю;

2) транспонувати матрицю S:

3) задати за допомогою ранжованої змінної цикл:

4) за допомогою функції почергово відсортувати всі стовпчики транспонованої матриці

5) транспонувати отриману матрицю

5.13.3. Основні матричні операції

Елементи матриць можна додавати, віднімати, множити, ділити, підносити до степеня.

Приклади. Задано дві матриці R i P. Виконати додавання, віднімання, множення, піднесення до степеня матриць, обчислення виразів із використанням констант і матриць.

Розв’язок.

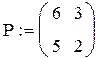
5.14. Розв’язування системи лінійних алгебраїчних рівнянь (СЛАР)

Існує кілька способів для роз’язування СЛАР.

1. Матричний метод, в основу якого покладено прямий метод Крамера.

Приклад. Задано СЛАР

X+Y+Z=1

X-4Y+Z=3

5X-Y+3Z=10

Обчислити значення змінних X, Y, Z.

Постановка задачі.

Цю систему слід переписати у матричному вигляді: у вигляді матриці коефіціентів, вектора невідомих та вектора правих частин.

K= N= PR=

Задану СЛАР можна замінити тотожним їй матричним виразом K*N=PR, звідки вектор невідомих вектор обчислюється за формулою

N= K^-1*PR.

Розв‘язок.

K:= PR:= N:=K^-1*PR

2. Функція lsolve дозволяє також визначити значення невідомих СЛАР.

У перший маркер функції заноситься ім’я матриці коефіціентів, у другий – ім’я вектора правих частин.

Lsolve(K,PR)=

3. Використання блока GIVEN - FIND, в основу якого покладено ітераційні методи, що застосовуються для великих СЛАР.

Для розвязку СЛАР цим способом слід виконати такі дії:

-ввести з клавіатури оператор GIVEN;

- ввести всі рівняння. Знак “ = ” в кожному з них вводиться при натиснутій клавіші Ctrl;

-ввести оператор FIND, в дужках якого через коми ввести змінні, а після дужок - символ “® ”.

Після символа “® ” виводиться вектор, що містить розв’язок.

Приклад. Розв’язати СЛАР

X+2Y+3Z=6

4X+2Y+Z=6

2X+3Y+Z=6

Розв’язок.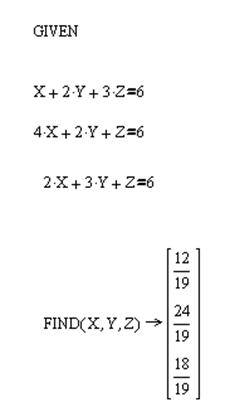

Дата добавления: 2014-01-13