Группы подстановок

ПРИМЕРЫ АЛГЕБРАИЧЕСКИХ СИСТЕМ

Рассмотрим некоторые алгебраические системы, наиболее часто встречающиеся в математике и прикладных областях.

Рассмотрение некоторых систем начнем с группы подстановок, общее описание которых дано в (3.4). Групповая операция задается внутренним законом компо­зиции - композицией подстановок.

Нейтральным элементом в группе подстановок является тождественная подстановка е, а симметричным элементом для любой подстановки а — симметричная подстановка а^-1. Так как композиция подстановок не подчиняется коммутативному закону, то группа подстановок п-й степени при п >3 не коммута­тивна.

Если множество N конечно и содержит п чисел, то множество S всех подстановок п -й степени также конечно и содержит п! эле­ментов. Такая группа называется симметрической группой по­рядка п! (порядок группы определяется числом ее элементов).

Полгруппы симметрических групп называют группами подста­новок. К ним относятся единичная группа, содержащая только ней­тральный элемент (тождественную подстановку), и сама симметри­ческая группа. Однако, кроме этих тривиальных групп, имеется много подгрупп симметрической группы, являющихся группами подстановок. В частности, группу образует множество всех четных подстановок (знакопеременная группа). Множество всех подстановок переводящих какой-либо элемент в себя, также является группой.

Подгруппами симметрических групп исчерпываются по су­ществу все конечные группы. Имеет место следующая теорема.

теорема Кэли. всякая конечная группа порядка п изоморфна некоторой группе подстановок п -й сте­пени ее элементов.

Доказательство. Пусть множество 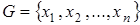с опре­деленным на нем законом композиции ┬ образует группу и 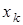- фиксированный элемент из G. Определим отображение, ставящее каждому элементу из G элемент , следующим образом:

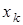┬ , i = 1, 2,....... п.

Это отображение взаимно-однозначно, так как при любом 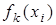соотношение ┬ 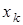имеет единственное решение 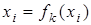┬ 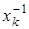, т.к. каждый элемент 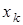группы имеет единственный симметричный ему 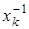. Таким обра­зом, взаимно-однозначное отображение 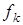на множестве G можно представить подстановкой п объектов 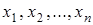, которая соот­ветствует элементу 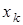, т. е.

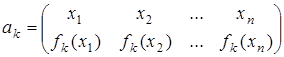
В этой подстановке нижняя перестановка 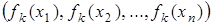- это строка матрицы композиции для элемента 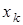. Прини­мая k = 1, 2,..., n, получаем п подстановок, соответствующих п элементам группы G. Нейтральному элементу отвечает тождест­венная подстановка е, симметричному элементу 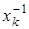- симмет­ричная подстановка .

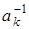Так как групповая операция ┬ по определению ассоциативна, то

┬ ┬ = ┬ (┬) = .

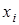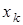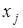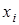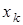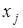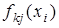С другой стороны,

┬ ┬ = (┬ ) ┬ = ┬ = .

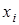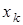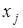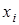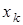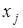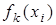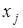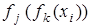Отсюда 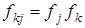, т. е. элементу 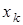┬ 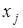соответствует композиция отображения 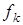и 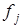, а значит, и композиция соответствующих им подстановок. Таким образом, множество подстановок образует группу порядка п, которая однозначно представляет группу G.

Например, группе третьего порядка с групповой операцией, заданной таблицей

соответствует группа подстановок 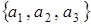, где

; ; .

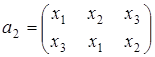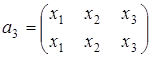Нейтральным элементом этой группы относительно определенного закона композиции является 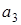, а подстановк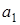и и 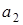- взаимно симметричные эле­менты (проверить самостоятельно). Если элементы исходной группы пронумеровать и заменить соответствующими им числами, то

; ; .

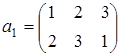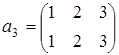Эта группа подстановок является подгруппой симметрической группы, которая, кроме указанных подстановок содержит подста­новки

; ; .

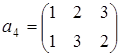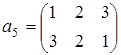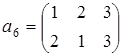каждая из которых обратна самой себе. Ясно, что при большом п для представления конечной группы п- го порядка используется лишь ничтожная часть перестановок симметрической группы.

Дата добавления: 2014-01-13