Кольцо множеств

Рассмотрим непустую систему множеств с операциями + и Ç. Нетрудно показать, что рассматриваемая система множеств образует кольцо, если для любых А и В этой системы А + В и А Ç В также принадлежат к этой системе множеств. Здесь опре­делены два внутренних закона композиции: дизъюнктивная сумма и пересечение. Нейтральным элементом относительно суммы служит пустое множество Æ, так как А + Æ = А. Симметричным для каждого А является само это множество, так как А + А = Æ.

Второй закон - ассоциативный и ди­стрибутивный относительно первого (см. 1.5).

Нейтральный элемент (единица) U относительно второго за­кона (пересечения) определяется соотношением A Ç U = А, откуда следует, что U есть не что иное, как максимальное множество этой системы, содержащее все другие входящие в систему множества (универсум U). Если такой элемент существует, то имеем кольцо с единицей (унитарное кольцо). Так, унитарное кольцо образует система всех подмножеств произвольного множества U. Примером кольца (без единицы) может служить множество всех ограниченных отрезков числовой прямой (не существует ограниченного отрезка, который служил бы единицей кольца, т. е. содержал все ограни­ченные отрезки прямой).

Так как для любых А и В справедливы соотношения:

А È В = (А + В) + (А + В) и А В = А + (А Ç В),

то кольцо мно­жеств содержит также А È В и А В. Говорят, что кольцо зам­кнуто относительно объединения и пересечения, разности и дизъюнк­тивной суммы.

7.4. Множество классов вычетов по модулю т

Как было пока­зано в (4.3), сравнение по модулю т есть отношение эквивалентности на множестве (кольце) целых чисел. Множество всех целых чисел разбивается на т классов эквивалентности 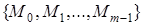, причем класс 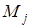объединяет числа 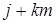(k - произвольное целое число), вычеты которых равны j. Совокупность классов вычетов по модулю т определяется системен представителей j = 0, 1, 2,..., т -1.

Сумма (произведение) двух классов вычетов по модулю т опре­деляется как класс, который содержит сумму (произведение) пред­ставителей этих классов. Поэтому действия над классами можно представить как арифметические действия над их представителями по модулю т. Например, при т =4 сложение и умножение зада­ется таблицами (числа являются представителями классов):

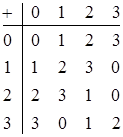
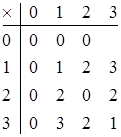
Сложение классов вычетов ассоциативно и коммутативно. Су­ществует нейтральный элемент 0 (j +0 = j), и каждый элемент j имеет симметричный ему 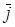такой, что j+ 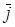= 0 (mod т). Так, для представителей 0, 1, 2, 3 симметричными являются соответ­ственно 0, 3, 2, 1. Отсюда следует, что множество классов вычетов при любом т образуют абелеву группу относительно сложения.

Умножение классов вычетов также ассоциативно и коммутатив­но. Существует нейтральный элемент 1 (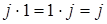).Но относительно умножения не каждый элемент j имеет симметричный, такой, что j ×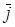= 1 (mod т). Действительно, как видно из таблицы, при т = 4 это соотношение имеет место только для 1 и 3, поскольку 1×l=l (mod 4) и 3×3=9=1 (mod 4), т. е. 1 и 3 симметричны са­мим себе, а элементы 0 и 2 не имеют симметричных. Следовательноi, множество классов вычетов относительно умножения не явля­ется группой, а образует моноид (полугруппу).

Можно доказать, что, если т - простое число, то каждый отличный от нуля элемент j имеет симметричный ему 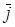и относительно умножения классов вычетов по модулю т.

Таким образом, множество классов вычетов по модулю от отно­сительно первого закона композиции (сложения) и второго закона (умножения) при любом т образует абелево кольцо с единицей, а при простых т - поле.

Дата добавления: 2014-01-13