Соотношение неопределенностей

В классической механике состояние частицы описывается так называемыми динамическими переменными: импульсом, энергией, значениями координат.

Своеобразие квантовой частицы состоит в том, что нельзя говорить о ее движении по определенной траектории и неправомерно говорить об одновременно точных значениях ее координаты х и импульса . Это следует из корпускулярно-волнового дуализма. Микрочастица с определенным импульсом имеет полностью неопределенную координату и наоборот, если микрочастица находится в состоянии с точным значением координаты, то ее импульс является полностью неопределенным.

Согласно соотношению неопределенностей Гейзенберга, открытому в 1927 г., неопределенности координат и соответствующих проекций импульса удовлетворяют условиям:

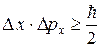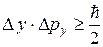, , . (7.3)

Вводится также соотношение неопределенностей для Е и t:

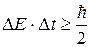. (7.4)

где D Е – неопределенность энергии некоторого состояния системы, D t – промежуток времени, в течение которого оно существует. Следовательно, система, имеющая среднее время жизни D t, не может быть охарактеризована определенным значением энергии, разброс энергии возрастает с уменьшением среднего времени жизни.

Поясним соотношение неопределенностей на следующем примере. Пусть на пути частицы расположена щель шириной . До прохождения через щель частица двигалась вдоль оси Y, поэтому составляющая импульса , так что , а ее координата x была совершенно неопределенной.

В момент прохождения частицы через щель ее положение в направлении вдоль оси Х определяется с точностью до ширины щели . В этот же момент вследствие дифракции частица отклоняется от первоначального направления и будет двигаться в пределах угла 2 j, соответствующего первому дифракционному минимуму. Следовательно, появляется неопределенность в значении составляющей импульса вдоль оси Х: . Так как первый минимум соответствует углу j, удовлетворяющему условию получим

по порядку величины совпадает с .

Невозможность одновременно точно определить координату и соответствующую проекцию импульса не связана с несовершенством методов измерения или измерительных приборов, а является следствием специфики микрообъектов. Так как в классической механике принимается, что измерение координаты и импульса может быть произведено с любой точностью, то соотношение неопределенностей является квантовым ограничением применимости классической механики к микрообъектам.

Учитывая, что 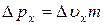, получим из соотношения Гейзенберга

.

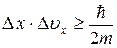Отсюда следует, что чем больше m, тем меньше неопределенность x и , и тем с большей степенью точности можно применять к этой частице понятие траектории. Так, например, уже для пылинки и линейными размерами 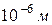, координата которой определена с точностью , неопределенность скорости , т.е. не будет сказываться при всех скоростях, с которыми может двигаться пылинка.

Применим соотношение неопределенностей к электрону, движущемуся в атоме водорода. Если неопределенность координаты электрона 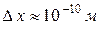(порядка размеров самого атома), то . Согласно законам классической физики при движении электрона вокруг ядра по круговой орбите радиуса его скорость . Таким образом, неопределенность скорости порядка самой скорости. Очевидно, в данном случае нельзя говорить о движении электрона в атоме по определенной траектории, иными словами, для описания движения электрона в атоме нельзя пользоваться законами классической физики.

Дата добавления: 2014-01-13