Потенциальный баpьеp. Туннельный эффект

Пpохождение частицы чеpез одномеpный

Различие в поведении квантовых и классических частиц проявляется в том случае, если на пути частицы встречается потенциальный барьер (при , при )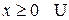

При данных условиях задачи классическая частица, обладая Е (полная энергия частицы), либо беспрепятственно пройдет над барьером (при E > U), либо отразится от него (при E < U) и будет двигаться в обратную сторону. Для микрочастицы же, даже при , имеется отличная от нуля вероятность, что она отразится от барьера. При 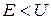имеется также отличная от нуля вероятность, что частица окажется в области x > l, т.е. проникнет сквозь барьер. Подобные выводы следуют из решения уравнения Шредингера для стационарных состояний. Рассмотрим случай 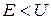, тогда для областей 1 и 3 имеем

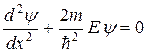
для области 2

.

Общие решения этих дифференциальных уравнений:

(для области 1)

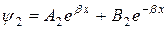(для области 2)

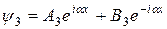(для области 3)

где , .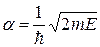

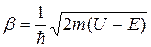Решение вида соответствует волне, распространяющейся в положительном направлении оси х, а решение вида - волне, распространяющейся в противоположном направлении. В области 3 имеется только волна, прошедшая сквозь барьер и распространяющаяся слева направо. Поэтому коэффициент следует принять равным нулю. Для нахождения остальных коэффициентов воспользуемся условиями, которым должна удовлетворять функция y. 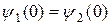Для того чтобы y была непрерывна во всей области изменений х от - ¥ до + ¥, должны выполняться условия: и 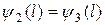. Для того чтобы y была гладкой, т.е. не имела изломов, должны выполняться условия: и .

Отношение квадратов модулей амплитуд отраженной и падающей волны

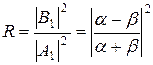(7.11)

определяет вероятность отражения частицы от потенциального барьера и называется коэффициентом отражения.

Отношение квадратов модулей амплитуд прошедшей и падающей волны

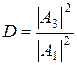
определяет вероятность прохождения частицы через барьер и называется коэффициентом прохождения (прозрачности). Для барьера конечной ширины

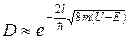(7.12)

В случае барьера произвольной формы

При преодолении потенциального барьера частица как бы проходит через «туннель» в нем, в связи с чем данное явление называется туннельным эффектом. С классической точки зрения туннельный эффект представляется абсурдным, так как частица в туннеле должна была бы обладать отрицательной кинетической энергией 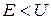. Однако туннельный эффект – явление специфически квантовое. В квантовой же механике деление полной энергии на кинетическую и потенциальную не имеет смысла, так как противоречит соотношению неопределенностей.

Поверхность металла является потенциальным барьером, который электроны преодолевают на глубину 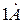и возвращаются обратно.

Дата добавления: 2014-01-13