Метрические пространства

Условия равновесия системы пар сил

- векторная форма (8.9)

- в проекциях на оси координат (8.10)

Одной из важнейших операций анализа является предельный переход. В основе этой операции лежит тот факт, что на числовой прямой определено расстояние от одной точки до другой. Многие фундаментальные факты анализа не связаны с алгебраической природой действи­тельных чисел (т. е. с тем, что они образуют поле), а опираются лишь на понятие расстояния. Обобщая представление о действи­тельных числах как о множестве, в котором введено расстояние между элементами, мы приходим к понятию метрического пространства - одному из важнейших понятий современной математики.

Метрическим пространством называется пара (Х, r), состоящая из некоторого множества (пространства) Х элементов (точек) и расстояния, т. е. неотрица­тельной действительной функции r(х,у), определенной для лю­бых х и у из Х и подчиненной следующим трем аксиомам:

1) r(х, у) = 0 тогда и только тогда, когда х = у,

2) r(х, у) = r(у, х) (аксиома симметрии),

3) r(х, г) ≤ r(х, у) + r (у, г) (аксиома треугольника).

Само метрическое пространство, т. е. пару (Х, ρ), мы будем обозначать, как правило, одной буквой:

R = (X, ρ).

В случаях, когда недоразумения исключены, мы будем за­частую обозначать метрическое пространство тем же символом, что и сам «запас точек» X.

Приведем примеры метрических пространств. Некоторыеизэтих пространств играют в анализе весьма важную роль.

1. Положив для элементов произвольного множества

мы получим, очевидно, метрическое пространство. Его можно на­звать пространством изолированных точек.

2. Множество действительных чисел с расстоянием

ρ(х, у) = | х - у |

образует метрическое пространство R ¹.

3. Множество упорядоченных наборов из п действительных чи­сел 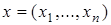с расстоянием

называется п -мерным арифметическим евклидовым пространством R ⁿ.

4. Рассмотрим то же самое множество наборов из п действительных чи­сел , но расстояние опре­делим в нем формулой

Справедливость аксиом 1)-3) здесь очевидна. Обозначим это метрическое пространство символом R ⁿ ₁.

5. Возьмем снова то же самое множество, что и в приме­рах 3 и 4, и определим расстояние между его элементами фор­мулой

Справедливость аксиом 1)-3) очевидна. Это пространство, ко­торое мы обозначим R ⁿ _¥ во многих вопросах анализа не менее удобно, чем евклидово пространство R ⁿ.

Последние три примера показывают, что иногда и в самом деле важно иметь различные обозначения для самого метриче­ского пространства и для множества его точек, так как один и тот же запас точек может быть по-разному метризован.

6. Множество С [a, b] всех непрерывных действительных функ­ций, определенных на отрезке [a, b] с расстоянием

также образует метрическое пространство. Аксиомы1)-3) про­веряются непосредственно. Это пространство играет очень важ­ную роль в анализе. Мы будем его обозначать тем же симво­лом С [a, b], что и само множество точек этого пространства.

7. Рассмотрим, как и в примере 6, совокупность всех функ­ций, непрерывных на отрезке С [a, b], но расстояние определим иначе, а именно, положим

Такое метрическое пространство мы будем обозначать С ₂ [a, b] и называть пространством непрерывных функций с квад­ратичной метрикой.

Дата добавления: 2014-01-13