Топологические пространства

Пусть Х - некоторое множество - пространство-носитель. Топологией в Х называется любая система τ его подмножеств G, удовлетворяющая следующим требованиям:

1. Само множество Х и пустое множество Æ принадлежат t.

2. Объединение 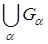любого (конечного или бесконечного) числа множеств из τ принадлежит τ.

3. пересечение 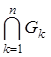любого конечного числа множеств из τ принадлежит τ.

Множество Х с заданной в нем топологиейτ, т.е. пара (X, τ ),называется топологическим пространством.

Множества, принадлежащие системеτ, называются открытыми.

Так же как метрическое пространство есть совокупность мно­жества точек - «носителя» - и введенной в этом множестве мет­рики, топологическое пространство есть совокупность множества точек и введенной в нем топологии. Таким образом, задать топо­логическое пространство - это значит задать некоторое множе­ство Х и задать в нем топологию τ, т. е. указать те подмноже­ства, которые считаются в Х открытыми.

Ясно, что в одном и том же множестве Х можно вводить разные топологии, превращая его тем самым н различные топо­логические пространства. И все же топологическое пространство, т. е. пару (Х, τ ), мы будем обозначать одной буквой, скажем, Т.

Элементы топологического пространства мы будем называть точ­ками.

Множества Т - G, дополнительные к открытым, называются замкнутыми множествами топологического пространства Т. Из аксиом 1 и 2 в силу соотношений двойственности вытекает, что:

1. Пустое множество Æ и все Т замкнуты.

2. Пересечение любого (конечного или бесконечного) числа и сумма конечного числа замкнутых множеств замкнуты.

На основе этих определений во всяком топологическом пространстве вводятся понятия окрестности, точки при­косновения, замыкания множества и др.

Окрестностью точки х Î Т называется всякое открытое множество G Ì Т, содержащее точку х. точка х Î Т называется точкой прикосновения множества М Ì Т, если каждая окрестность точки х содержит хотя бы одну точку из М; х называется предельной точкой множества М, если каждая окрестность точки х содержит хотя бы одну точку из М, отличную от х. Совокупность точек прикосновения множества М называется замыканием множества М и обозначается символом [М]. Легко доказать, что замкнутые множества (определенные нами выше как дополнения открытых), и только они, удовлетворяют условию [М] = М. [М] есть наименьшее замкнутое множество, содержащее М.

Рассмотрим примеры топологических пространств.

1. Пусть Т - произвольное множество. Будем считать открытыми все его подмножества. Аксиомы 1 и 2 при этом, очевидно, выполнены, т. е. мы действительно получаем топологическое пространство. В нем все множества одновременно и открыты и замкнуты, и, значит, каждое из них совпадает со своим замыканием. Такой дискретной топологией обладает, например, метрическое пространство, указанное в примере 1 п. 1.

2. В качестве другого крайнего случая рассмотрим в произвольном множестве Т тривиальную топологию, состоящую всего из двух множеств: всего Т и пустого множества Æ. Здесь замыкание каждого непустого множества есть все Т. Такое топологическое пространство можно назвать «пространством слипшихся точек».

3. Пусть Т состоит из двух точек а и b, причем открытыми множествами мы считаем все Т, пустое множество и множество, состоящее из одной точки b. Аксиомы 1 и 2 здесь выполнены. В этом пространстве (которое часто называют связным двоеточием) замкнуты такие подмножества: все Т, пустое множество и точка а. Замыкание одноточечного множества [b] есть все Т.

4. Во всяком метрическом пространстве можно ввести топологию, взяв в качестве базы открытых множеств e-окрестности точек х этого пространства:

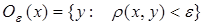
Дата добавления: 2014-01-13