
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Линейные пространства
|
|
|
|
Непустое множество L называется линейным, или векторным, пространством, если оно удовлетворяет следующим условиям:
I. Для любых двух элементов х, у Î L однозначно определен третий элемент z Î L, называемый их суммой и обозначаемый х + у, причем
1) х + у = у + х (коммутативность),
2) х + (у + z) = (х+ у) + z (ассоциативность),
3) в L существует такой элемент 0, что х + 0 = х для всех x Î L (существование нуля),
4) для каждого x Î L существует такой элемент - х, что х + (- х) = 0 (существование противоположного элемента).
II. Для любого числа α и любого элемента х Î L определен элемент ax Î L (произведение элемента х на число a), причем
1) a(bх)=(ab)х,
2) 1 · х=х
3) (a + b)х = ax + bx,
4) a(х+у) = aх + aу.
В зависимости от того, какой запас чисел (все комплексные или только действительные) используется, различают комплексные и действительные линейные пространства. Заметим, что всякое комплексное линейное пространство можно рассматривать как некоторое действительное пространство, если ограничиться в нем умножением векторов на действительные числа.
Рассмотрим некоторые примеры линейных пространств.
1. Прямая линия R 1, т. е. совокупность действительных чисел с обычными арифметическими операциями сложения и умножения, представляет собой линейное пространство.
2. Совокупность всевозможных упорядоченных наборов из п действительных чисел 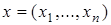 , где сложение и умножение на число определяются покоординатно, также является линейным пространством. Оно называется действительным п-мерным арифметическим пространством и обозначается символом R n. Аналогично, комплексное п -мерное арифметическое пространство С n определяется как совокупность наборов п комплексных чисел (с умножением на любые комплексные числа).
, где сложение и умножение на число определяются покоординатно, также является линейным пространством. Оно называется действительным п-мерным арифметическим пространством и обозначается символом R n. Аналогично, комплексное п -мерное арифметическое пространство С n определяется как совокупность наборов п комплексных чисел (с умножением на любые комплексные числа).
3. Непрерывные (действительные или комплексные) функции на некотором отрезке [a,b] с обычными операциями сложения функций и умножения их на числа образуют линейное пространство С [a, b], являющееся одним из важнейших в математическом анализе.
Линейные пространства L и L* называются изоморфными, если между их элементами можно установить взаимно однозначное соответствие, которое согласовано с операциями в L и L*. Это означает, что из

следует
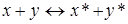 и
и 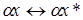 ,
,
где α - произвольное число.
Изоморфные пространства можно рассматривать как различные реализации одного и того же пространства. Примерами изоморфных линейных пространств могут служить арифметическое п -мерное пространство (действительное или комплексное) и пространство всех многочленов степени п -1 (соответственно с действительными или комплексными коэффициентами) с обычными операциями сложения многочленов и умножения их на числа.
|
|
|
|
|
Дата добавления: 2014-01-13; Просмотров: 420; Нарушение авторских прав?; Мы поможем в написании вашей работы!