Пример 2.1. Оптимальное распределение ресурса для центра

Фирма занимается производством делимого продукта. Руководство фирмы (центр) заключило договор на производство продукта количеством R =150 единиц. Этот заказ могут выполнить два подразделения фирмы (агента). Цена единицы продукции p =4000 руб. Функции затрат агентов, соответственно равны 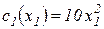и .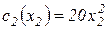

Определить:

1. оптимальное распределение заказа между подразделениями фирмы, в интересах центра;

2. максимальную прибыль агентов и центра.

Решение:

Сформулируем математическую постановку задачи. Запишем целевую функцию центра:

. (2.8)

Сумма планов для агентов должна быть равна заказу, полученному центром:

(2.9)

Оптимизационная задача (2.8)-(2.9) является задачей на условный экстремум. Её решение можно найти двумя способами.

I способ: р ешение методом подстановки.

Выразим план для второго агента из ограничения (2.9) и подставим в целевую функцию центра:

. (2.10)

Таким образом, от задачи с двумя переменными и ограничением (2.8)-(2.9) перешли к задаче с одной переменной (2.10).

Для нахождения экстремума функции одной переменной продифференцируем и приравняем к 0 выражение (2.10):

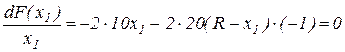. (2.11)

Решая уравнение (2.11), получим план для первого агента:

.

Из ограничения (2.9) определим план для второго агента:

.

II способ: решение методом множителей Лагранжа.

Перепишем ограничение (2.9) в следующем виде:

. (2.12)

Запишем функцию Лагранжа как сумму целевой функции (2.8) и ограничения (2.11), умноженного на множитель Лагранжа :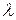

.

Найдём частные производные от функции Лагранжа по неизвестным переменным 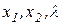и приравняем к нулю:

Отнимем из первого уравнения второе, множитель Лагранжа сократится, получим систему из двух уравнений:

Решая полученную систему, определим планы для первого и второго агентов:

Определим максимальную прибыль центра:

Определим прибыль для первого и второго агента:

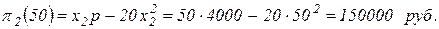
Дата добавления: 2014-01-13