
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Умножение вероятностей
|
|
|
|
Определение 2.3. Произведением 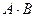 двух событий
двух событий  и
и  называется событие, состоящее в одновременном появлении и события
называется событие, состоящее в одновременном появлении и события  и события
и события  . Произведение двух событий
. Произведение двух событий  и
и  , согласно теоретико-множественным представлениям называется пересечение этих событий
, согласно теоретико-множественным представлениям называется пересечение этих событий 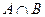 .
.
Определение 2.5. Два события называются независимыми, если появление одного из них не меняет вероятность появления другого. В противном случае события называются зависимыми.
Определение 2.6. Несколько событий называются независимыми в совокупности, если независимы любые два из них и независимы любые из данных событий и любые комбинации (произведения) остальных событий. В противном случае события называются зависимыми.
Определение 2.7. Вероятность наступления события  , вычисленная при условии наступления другого события
, вычисленная при условии наступления другого события  , называется условной вероятностью события
, называется условной вероятностью события  по отношению к событию
по отношению к событию  . Записывается это либо
. Записывается это либо 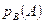 , либо
, либо 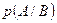 .
.
Теорема 2.3. Вероятность совместного появления двух зависимых событий равна произведению вероятностей одного из них на условную вероятность другого, найденную из предположения о том, что первое событие уже произошло:
 (2.6)
(2.6)
Данная теорема распространяется и на большее число событий:
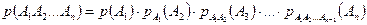 (2.7)
(2.7)
Докажем теорему 2.3. Пусть даны два события  и
и  такие, что
такие, что 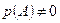 и
и 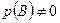 . Из всех всевозможных исходов
. Из всех всевозможных исходов 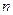 событию
событию  благоприятствуют
благоприятствуют 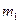 исходов, событию
исходов, событию  –
– 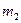 исхода, а событию
исхода, а событию 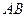 –
– 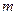 (рис. 2.2). Вероятности событий
(рис. 2.2). Вероятности событий  ,
,  и
и 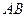 соответственно равны
соответственно равны 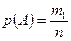 ,
, 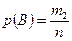 ,
, 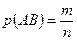 . Найдем условную вероятность события
. Найдем условную вероятность события 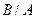 . Событию
. Событию 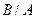 соответствуют
соответствуют 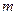 благоприятных исходов из
благоприятных исходов из 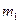 всевозможных исходов. Тогда
всевозможных исходов. Тогда 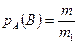 . Разделим числитель и знаменатель на
. Разделим числитель и знаменатель на 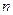 :
: 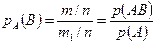 . Отсюда следует
. Отсюда следует  .
.
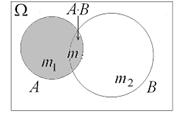
Рис. 2.2.
Рассмотрим следующий пример. Предположим, что мы подбросили игральный кубик. Событие  – выпало число «4». Вероятность такого события равна
– выпало число «4». Вероятность такого события равна  . Предположим, что мы не знаем, какое именно число выпало при подбрасывании, но знаем, что оно четное (событие
. Предположим, что мы не знаем, какое именно число выпало при подбрасывании, но знаем, что оно четное (событие  ). Информация о событии
). Информация о событии  уменьшает наше пространство событий, и поэтому меняет вероятность появления события
уменьшает наше пространство событий, и поэтому меняет вероятность появления события  . Полная группа событий для первоначального события
. Полная группа событий для первоначального события  представляет собой набор натуральных чисел от 1 до 6 включительно. Появление информации о том, что выпавшее число – четное (событие
представляет собой набор натуральных чисел от 1 до 6 включительно. Появление информации о том, что выпавшее число – четное (событие  ), уменьшило пространство событий в два раза (числа 2, 4, 6). Поэтому вероятность появления числа «4» при условии, что выпавшее число – четное, возрастает от 1/6 до 1/3.
), уменьшило пространство событий в два раза (числа 2, 4, 6). Поэтому вероятность появления числа «4» при условии, что выпавшее число – четное, возрастает от 1/6 до 1/3.
На основании теоремы 2.3 можем записать:
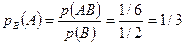
Теорема 2.4. Вероятность совместного появления двух независимых событий равна произведению вероятностей этих событий:
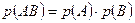 (2.8)
(2.8)
Данная теорема распространяется и на большее число событий:
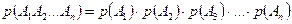 (2.9)
(2.9)
Пример 2.4. Производятся два выстрела по одной и той же мишени. Вероятность попадания в мишень при первом выстреле равна 0,7, при втором 0,9. Найти вероятность того, что будет хотя бы одно попадание.
Решение:
Пусть событие  состоит в том, что попадание произошло при первом выстреле, событие
состоит в том, что попадание произошло при первом выстреле, событие  – при втором. При этом
– при втором. При этом  = 0,7, а
= 0,7, а 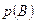 = 0,9. События
= 0,9. События  и
и  являются совместными и независимыми, следовательно:
являются совместными и независимыми, следовательно:
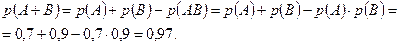
Пример 2.5. Из урны, в которой находятся 7 белых и 3 черных шара вынимают 2 шара. Найти вероятность того, что оба шара окажутся черными. Испытания будем проводить по двум схемам: 1) шары возвращаются в корзину; 2) шары не возвращаются в корзину.
Решение:
1) События  и
и  состоят соответственно вытащить из урны черный шар в первый и во второй. При таком испытании, когда извлеченный шар обратно возвращается, данные события совместные и независимые. Тогда
состоят соответственно вытащить из урны черный шар в первый и во второй. При таком испытании, когда извлеченный шар обратно возвращается, данные события совместные и независимые. Тогда 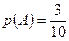 ;
; 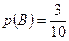 . Вероятность того, что оба шара будут черного цвета, равна:
. Вероятность того, что оба шара будут черного цвета, равна: 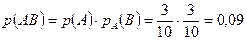 .
.
2) События  и
и  состоят соответственно вытащить из урны черный шар в первый и во второй. При таком испытании, когда извлеченный шар обратно не возвращается, данные события совместные и зависимые. Тогда
состоят соответственно вытащить из урны черный шар в первый и во второй. При таком испытании, когда извлеченный шар обратно не возвращается, данные события совместные и зависимые. Тогда 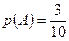 ;
; 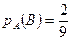 . После того как из урны извлекли первый черный шар, то в ней осталось всего 9 шаров, из которых только два окрашены в черный цвет. Таким образом:
. После того как из урны извлекли первый черный шар, то в ней осталось всего 9 шаров, из которых только два окрашены в черный цвет. Таким образом: 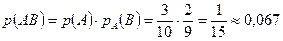 .
.
Если события 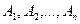 независимы в совокупности, то и противоположные к ним события
независимы в совокупности, то и противоположные к ним события 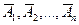 также независимы в совокупности.
также независимы в совокупности.
Если несколько событий независимы попарно, то отсюда еще не следует их независимость в совокупности. В этом смысле требование независимости в совокупности сильнее требования их попарной независимости.
Поясним сказанное на примере. Пусть в урне имеется 4 окрашенных шара: красный ( ), синий (
), синий ( ), черный (
), черный (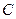 ) и один во все эти три цвета (
) и один во все эти три цвета (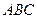 ). Чему равна вероятность того, что извлеченный из урны шар имеет красный цвет?
). Чему равна вероятность того, что извлеченный из урны шар имеет красный цвет?
Так как из четырех шаров два имеют красный цвет, то  = 2/4 = 1/2. Рассуждая аналогично, найдем
= 2/4 = 1/2. Рассуждая аналогично, найдем 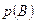 = 1/2,
= 1/2, 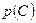 = 1/2. Допустим теперь, что взятый шар имеет синий цвет, т. е. событие
= 1/2. Допустим теперь, что взятый шар имеет синий цвет, т. е. событие  уже произошло. Изменится ли вероятность того, что извлеченный шар имеет красный цвет, т. е. изменится ли вероятность события
уже произошло. Изменится ли вероятность того, что извлеченный шар имеет красный цвет, т. е. изменится ли вероятность события  ? Из двух шаров, имеющих синий цвет, один шар имеет и красный цвет, поэтому вероятность события
? Из двух шаров, имеющих синий цвет, один шар имеет и красный цвет, поэтому вероятность события  по-прежнему равна 1/2. Другими словами, условная вероятность события
по-прежнему равна 1/2. Другими словами, условная вероятность события  , вычисленная в предположении, что наступило событие
, вычисленная в предположении, что наступило событие  , равна его безусловной вероятности. Следовательно, события
, равна его безусловной вероятности. Следовательно, события  и
и  независимы. Аналогично придем к выводу, что события
независимы. Аналогично придем к выводу, что события  и
и 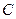 ,
,  и
и 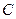 независимы. Итак, события
независимы. Итак, события  ,
,  и
и 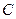 попарно независимы. Независимы ли эти события в совокупности? Оказывается, нет. Действительно, пусть извлеченный шар имеет два цвета, например синий и черный. Чему равна вероятность того, что этот шар имеет и красный цвет? Лишь один шар окрашен во все три цвета, поэтому взятый шар имеет и красный цвет. Таким образом, допустив, что события
попарно независимы. Независимы ли эти события в совокупности? Оказывается, нет. Действительно, пусть извлеченный шар имеет два цвета, например синий и черный. Чему равна вероятность того, что этот шар имеет и красный цвет? Лишь один шар окрашен во все три цвета, поэтому взятый шар имеет и красный цвет. Таким образом, допустив, что события  и
и 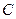 произошли, приходим к выводу, что событие
произошли, приходим к выводу, что событие  обязательно наступит. Следовательно, это событие достоверное и вероятность его равна единице. Другими словами, условная вероятность
обязательно наступит. Следовательно, это событие достоверное и вероятность его равна единице. Другими словами, условная вероятность 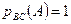 события
события  не равна его безусловной вероятности
не равна его безусловной вероятности  =1/2. Итак, попарно независимые события
=1/2. Итак, попарно независимые события  ,
,  и
и 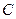 не являются независимыми в совокупности.
не являются независимыми в совокупности.
|
|
|
|
|
Дата добавления: 2014-01-13; Просмотров: 448; Нарушение авторских прав?; Мы поможем в написании вашей работы!